Trapezfläche funktional
Dieses GeoGebra-Applet bezieht sich auf folgenden Artikel:
Roth, J. (2008). Systematische Variation – Eine Lernumgebung vernetzt Geometrie und Algebra. Mathematik lehren, 146, 17-21
Erkundungsaufträge
(1) Form erkunden − Begriffe bilden
Variiere mit Hilfe der Schieberegler für a, c und h und durch Ziehen am Punkt C die Trapezform.
 Flächeninhalt angeklickt
Flächeninhalt angeklickt  und anschließend das gewünschte Viereck
ausgewählt
und anschließend das gewünschte Viereck
ausgewählt  werden.
b) Kannst du die Flächeninhaltsformel für das Trapez entsprechend umformen?
Hinweis:
Bei Problemen können dir die Ergebnisse aus "(1) Form erkunden − Begriffe bilden"
evtl. weiterhelfen.
(3) Grenzfälle untersuchen
Die Variablen a, c und h in der Flächeninhaltsformel
werden.
b) Kannst du die Flächeninhaltsformel für das Trapez entsprechend umformen?
Hinweis:
Bei Problemen können dir die Ergebnisse aus "(1) Form erkunden − Begriffe bilden"
evtl. weiterhelfen.
(3) Grenzfälle untersuchen
Die Variablen a, c und h in der Flächeninhaltsformel
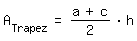 des Trapezes ABCD bezeichnen jeweils Streckenlängen und können keine negativen Werte annehmen.
des Trapezes ABCD bezeichnen jeweils Streckenlängen und können keine negativen Werte annehmen.  Trapez
Trapez  1):
1):
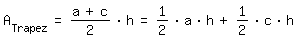
 Koordinaten
Koordinaten  (h|A) aus und variiere h mit dem entsprechenden Schieberegler.
(h|A) aus und variiere h mit dem entsprechenden Schieberegler.
- Welche Sonderfälle kannst du so herstellen?
- Was bedeutet das für die Beziehung zwischen den Viereckstypen?
![]() a) Wie lauten die entsprechenden Formeln für
- ein Dreieck?
- ein Parallelogramm?
- ein Rechteck?
- ein Quadrat?
a) Wie lauten die entsprechenden Formeln für
- ein Dreieck?
- ein Parallelogramm?
- ein Rechteck?
- ein Quadrat?
- Was passiert im Grenzfall, wenn a, c oder h gleich Null wird?
- Kannst du die ausmultiplizierte Formel geometrisch interpretieren?
- Wird er größer, wird er kleiner oder bleibt er gleich?
- Verändert er sich, genau wie die Höhe h auch gleichmäßig oder manchmal schneller und manchmal langsamer? Hinweis: Du kannst diese Frage z. B. mit Hilfe von geometrischen Überlegungen klären.
- Was beobachtest du?
- Welcher funktionale Zusammenhang besteht also zwischen h und dem Flächeninhalt A des Trapezes?
Hinweis:
Du kannst den zugehörigen Funktionsgraph über
 Koordinaten
Koordinaten  A(h) einblenden.
A(h) einblenden.
- Kannst du bei der Variation von h am Graphen besondere Eigenschaften des funktionalen Zusammenhangs entdecken?
- Überlege, warum gerade dieser funktionale Zusammenhang besteht. Hinweis: Du kannst das z. B. geometrisch begründen.
- Kannst du die Flächeninhaltsformel für das Trapez so umformen, dass du den entdeckten Funktionstyp anhand des Funktionsterms erkennst?
- Was erwartest du, wie die Funktionsgraphen von A(a) und A(c) verlaufen? Schreibe deine Vermutung zunächst auf!
- Beantworte die Fragen aus dem Abschnitt "(5) Funktionale Zusammenhänge entdecken" auch für die Funktionen A(a) und A(c).
- Waren deine Vorhersagen richtig? Weißt du jetzt, warum die Graphen so verlaufen, wie unter
 Koordinaten
Koordinaten  A(a) bzw.
A(a) bzw.  A(c) dargestellt?
A(c) dargestellt?
- Variiere nun die drei Größen mit Hilfe der Schieberegler und beobachte die Veränderungen an den Funktionsgraphen. Kannst du deine Beobachtungen erklären?