Criterio de Congruencia.ALA (Hoja Dinámica)
Justificar sólidamente la validez de los siguientes enunciados.
1. ¿Es posible construir un triángulo sabiendo la medida de dos ángulos? 2. ¿Es posible construir un único triángulo sabiendo la medida de un lado y los ángulos adyacentes a ese lado? 3. ¿Se puede construir un triángulo sabiendo la medida de dos lados? 4. ¿Se puede construir un triángulo sabiendo la medida los tres lados? 5. ¿Cuáles son los criterios que permiten verificar que dos triángulos son congruentes?
Congruencia de triángulos.
En Geometría se usa la palabra congruentes para comparar dos figuras que son iguales. A las reglas para verificar si dos triángulos son congruentes usando el mínimo de sus elementos se les conoce como criterios de congruencia.
Criterios de congruencia.
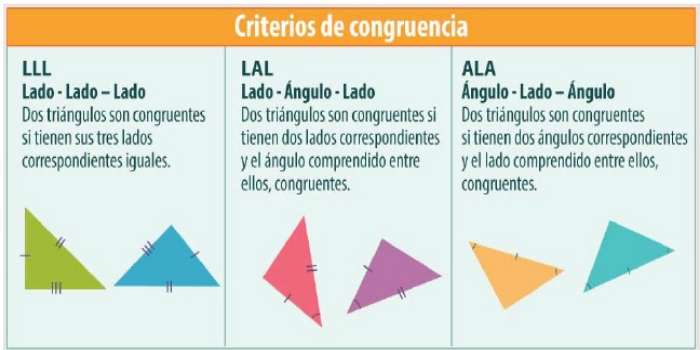
PRIMER CASO DE CONGRUENCIA DE TRIÁNGULOS
SEGUNDO CASO DE CONGRUENCIA DE TRIÁNGULOS.
TERCER CASO DE CONGRUENCIA
Actividad de Desarrollo.
1. Utilizando el programa Geogebra, construyan triángulos que cumplan con los siguientes datos:
a) Las longitudes de los lados son: 4 cm, 5 cm y 7 cm.
b) Las longitudes de los lados son 5 cm y 6 cm, y el ángulo comprendido es de 60°.
2. Verifiquen cómo son estos triángulos con respecto a los de sus compañeros.
Actividad de Cierre.
1) Demostrar que:
a) La altura de un triángulo isósceles acutángulo divide al triángulo en dos triángulos congruentes.
b) La diagonal de un rectángulo lo divide en dos triángulos congruentes.