Transformationen - Verschieben von Graphen
Mithilfe dieses digitalen Arbeitsblattes sollst du schrittweise Transformationen, d.h. "Veränderungen", an Funktionsgraphen untersuchen. Mithilfe des digitalen Arbeitsblattes kannst du Transformationen von Graphen erkunden und allgemeine Regeln herausfinden.
Es gibt verschiedene Arten von Transformationen. Wir beschäftigen uns mit dem Verschieben von Graphen (1. AB) und dem Strecken/Stauchen von Graphen (2. AB).
Wir beginnen mit dem Verschieben von Graphen.
Lies dir zunächst einmal folgende Erklärungen durch:
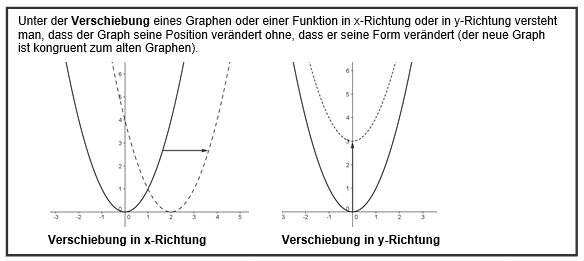
Man kann einen Graphen sowohl in x- als auch in y-Richtung verschieben. Starten wir mit...
1. Verschiebung in y-Richtung
Einen Graphen in y-Richtung, d.h. "nach oben" bzw. "nach unten", verschieben kannst du bereits. Mithilfe der folgenden Graphen, die GeoGebra dir anzeigt, kannst du dies noch einmal wiederholen.
Arbeitsauftrag: Zeichne mithilfe von GeoGebra jeweils den um 2 nach oben und um 3 nach unten verschobenen Graphen (links im Eingabefenster eingeben und auf Enter drücken).
Regel: Formuliere nun eine passende Regel: Die Verschiebung eines Graphen in y-Richtung erreicht man, indem man die Funktionsvorschrift folgendermaßen abändert:
2. Verschiebung in x-Richtung
Einen Graphen in x-Richtung, d.h. "nach links" bzw. "nach rechts", verschieben kennst du ebenfalls bereits von Parabeln.
Arbeitsauftrag: Zeichne mithilfe von GeoGebra jeweils den um 2 nach rechts und um 2 nach links verschobenen Graphen (links im Eingabefenster eingeben und auf Enter drücken).
Wie lässt sich dies nun auf eine allgemeine Funktion übertragen?
Versuche die folgende Funktion um jeweils 2 Einheiten nach rechts und links zu verschieben.
(Der Tipp unterhalb der beiden Funktionenfenster hilft dir, wenn du Hilfe brauchst.)
Tipp: Parabeln verschiebt man, indem man statt xz.B. (x-2) [Verschiebung um 2 nach rechts] oder (x+3) [Verschiebung um 3 nach links] schreibt. Ersetze das x in der Funktion ebenfalls durch eine Klammer +/- die Verschiebung.
Regel: Formuliere nun eine passende Regel: Die Verschiebung eines Graphen in x-Richtung erreicht man, indem man die Funktionsvorschrift folgendermaßen abändert:
Wenn du alle Aufgaben bearbeitet (und ggf. kontrolliert) hast, klicke auf Abgeben! :-)
Hinweis: Wenn noch einiges unklar geblieben ist, findest du im Schulbuch auf Seite 31-33 weitere Erklärungen und Beispiele.
Folgende Fragen sind offen geblieben: