Livro referente à Geometria e Trigonometria
Trigonometria
A trigonometria é a parte da matemática que estuda as relações existentes entre os lados e os ângulos dos triângulos.
Ela é utilizada também em outras áreas de estudo como física, química, biologia, geografia, astronomia, medicina, engenharia, etc.
Funções TrigonométricasAs funções trigonométricas são as funções relacionadas aos triângulos retângulos, que possuem um ângulo de 90°. São elas: seno, cosseno e tangente.
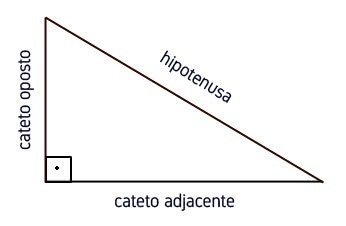 As funções trigonométricas estão baseadas nas razões existentes entre dois lados do triângulo em função de um ângulo.
Ela são formadas por dois catetos (oposto e adjacente) e a hipotenusa:
As funções trigonométricas estão baseadas nas razões existentes entre dois lados do triângulo em função de um ângulo.
Ela são formadas por dois catetos (oposto e adjacente) e a hipotenusa:
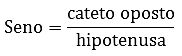 Lê-se cateto oposto sobre a hipotenusa.
Lê-se cateto oposto sobre a hipotenusa.
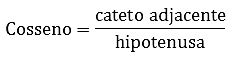 Lê-se cateto adjacente sobre a hipotenusa.
Lê-se cateto adjacente sobre a hipotenusa.
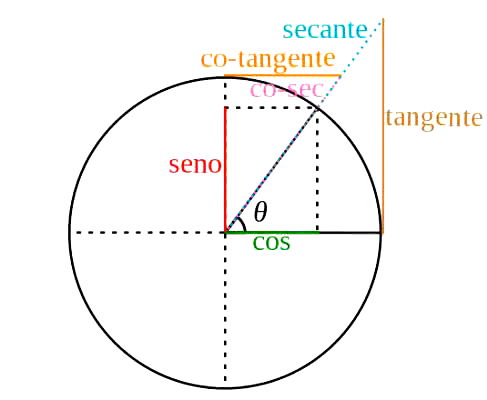
 Círculo TrigonométricoO círculo trigonométrico ou círculo unitário é usado no estudo das funções trigonométricas: seno, cosseno e tangente.
Círculo TrigonométricoO círculo trigonométrico ou círculo unitário é usado no estudo das funções trigonométricas: seno, cosseno e tangente.
 Teoria EuclidianaAlguns conceitos importantes da geometria euclidiana nos estudos da trigonometria são:
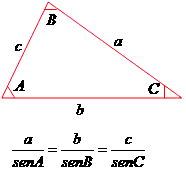
Lei dos SenosA Lei dos Senos estabelece que num determinado triângulo, a razão entre o valor de um lado e o seno de seu ângulo oposto, será sempre constante.
Dessa forma, para um triângulo ABC de lados a, b, c, a Lei dos Senos é representada pela seguinte fórmula:
Teoria EuclidianaAlguns conceitos importantes da geometria euclidiana nos estudos da trigonometria são:
Lei dos SenosA Lei dos Senos estabelece que num determinado triângulo, a razão entre o valor de um lado e o seno de seu ângulo oposto, será sempre constante.
Dessa forma, para um triângulo ABC de lados a, b, c, a Lei dos Senos é representada pela seguinte fórmula:
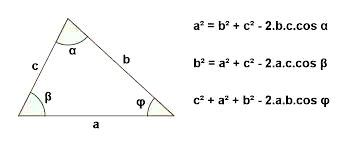
 Lei dos CossenosA Lei dos Cossenos estabelece que em qualquer triângulo, o quadrado de um dos lados, corresponde à soma dos quadrados dos outros dois lados, menos o dobro do produto desses dois lados pelo cosseno do ângulo entre eles.
Dessa maneira, sua fórmula é representada da seguinte maneira:
Lei dos CossenosA Lei dos Cossenos estabelece que em qualquer triângulo, o quadrado de um dos lados, corresponde à soma dos quadrados dos outros dois lados, menos o dobro do produto desses dois lados pelo cosseno do ângulo entre eles.
Dessa maneira, sua fórmula é representada da seguinte maneira:
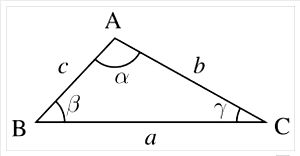
 Lei das TangentesA Lei das Tangentes estabelece a relação entre as tangentes de dois ângulos de um triângulo e os comprimentos de seus lados opostos.
Dessa forma, para um triângulo ABC, de lados a, b, c, e ângulos α, β e γ, opostos a estes três lados, têm-se a expressão:
Lei das TangentesA Lei das Tangentes estabelece a relação entre as tangentes de dois ângulos de um triângulo e os comprimentos de seus lados opostos.
Dessa forma, para um triângulo ABC, de lados a, b, c, e ângulos α, β e γ, opostos a estes três lados, têm-se a expressão:
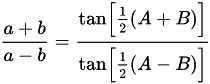 Teorema de PitágorasO Teorema de Pitágoras, criado pelo filósofo e matemático grego, Pitágoras de Samos, (570 a.C. - 495 a.C.), é muito utilizado nos estudos trigonométricos.
Ele prova que no triângulo retângulo, composto por um ângulo interno de 90° (ângulo reto), a soma dos quadrados de seus catetos corresponde ao quadrado de sua hipotenusa:
a2 = c2+ b2
Sendo,
a: hipotenusa
c e b: catetos
Teorema de PitágorasO Teorema de Pitágoras, criado pelo filósofo e matemático grego, Pitágoras de Samos, (570 a.C. - 495 a.C.), é muito utilizado nos estudos trigonométricos.
Ele prova que no triângulo retângulo, composto por um ângulo interno de 90° (ângulo reto), a soma dos quadrados de seus catetos corresponde ao quadrado de sua hipotenusa:
a2 = c2+ b2
Sendo,
a: hipotenusa
c e b: catetos
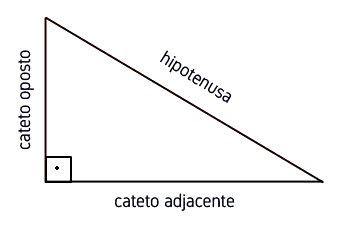
 As funções trigonométricas estão baseadas nas razões existentes entre dois lados do triângulo em função de um ângulo.
Ela são formadas por dois catetos (oposto e adjacente) e a hipotenusa:
As funções trigonométricas estão baseadas nas razões existentes entre dois lados do triângulo em função de um ângulo.
Ela são formadas por dois catetos (oposto e adjacente) e a hipotenusa:
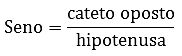 Lê-se cateto oposto sobre a hipotenusa.
Lê-se cateto oposto sobre a hipotenusa.
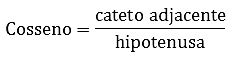 Lê-se cateto adjacente sobre a hipotenusa.
Lê-se cateto adjacente sobre a hipotenusa.
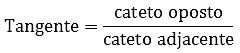 Círculo TrigonométricoO círculo trigonométrico ou círculo unitário é usado no estudo das funções trigonométricas: seno, cosseno e tangente.
Círculo TrigonométricoO círculo trigonométrico ou círculo unitário é usado no estudo das funções trigonométricas: seno, cosseno e tangente.
 Teoria EuclidianaAlguns conceitos importantes da geometria euclidiana nos estudos da trigonometria são:
Lei dos SenosA Lei dos Senos estabelece que num determinado triângulo, a razão entre o valor de um lado e o seno de seu ângulo oposto, será sempre constante.
Dessa forma, para um triângulo ABC de lados a, b, c, a Lei dos Senos é representada pela seguinte fórmula:
Teoria EuclidianaAlguns conceitos importantes da geometria euclidiana nos estudos da trigonometria são:
Lei dos SenosA Lei dos Senos estabelece que num determinado triângulo, a razão entre o valor de um lado e o seno de seu ângulo oposto, será sempre constante.
Dessa forma, para um triângulo ABC de lados a, b, c, a Lei dos Senos é representada pela seguinte fórmula:
 Lei dos CossenosA Lei dos Cossenos estabelece que em qualquer triângulo, o quadrado de um dos lados, corresponde à soma dos quadrados dos outros dois lados, menos o dobro do produto desses dois lados pelo cosseno do ângulo entre eles.
Dessa maneira, sua fórmula é representada da seguinte maneira:
Lei dos CossenosA Lei dos Cossenos estabelece que em qualquer triângulo, o quadrado de um dos lados, corresponde à soma dos quadrados dos outros dois lados, menos o dobro do produto desses dois lados pelo cosseno do ângulo entre eles.
Dessa maneira, sua fórmula é representada da seguinte maneira:
 Lei das TangentesA Lei das Tangentes estabelece a relação entre as tangentes de dois ângulos de um triângulo e os comprimentos de seus lados opostos.
Dessa forma, para um triângulo ABC, de lados a, b, c, e ângulos α, β e γ, opostos a estes três lados, têm-se a expressão:
Lei das TangentesA Lei das Tangentes estabelece a relação entre as tangentes de dois ângulos de um triângulo e os comprimentos de seus lados opostos.
Dessa forma, para um triângulo ABC, de lados a, b, c, e ângulos α, β e γ, opostos a estes três lados, têm-se a expressão:

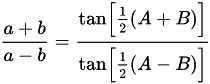 Teorema de PitágorasO Teorema de Pitágoras, criado pelo filósofo e matemático grego, Pitágoras de Samos, (570 a.C. - 495 a.C.), é muito utilizado nos estudos trigonométricos.
Ele prova que no triângulo retângulo, composto por um ângulo interno de 90° (ângulo reto), a soma dos quadrados de seus catetos corresponde ao quadrado de sua hipotenusa:
a2 = c2+ b2
Sendo,
a: hipotenusa
c e b: catetos
Teorema de PitágorasO Teorema de Pitágoras, criado pelo filósofo e matemático grego, Pitágoras de Samos, (570 a.C. - 495 a.C.), é muito utilizado nos estudos trigonométricos.
Ele prova que no triângulo retângulo, composto por um ângulo interno de 90° (ângulo reto), a soma dos quadrados de seus catetos corresponde ao quadrado de sua hipotenusa:
a2 = c2+ b2
Sendo,
a: hipotenusa
c e b: catetos

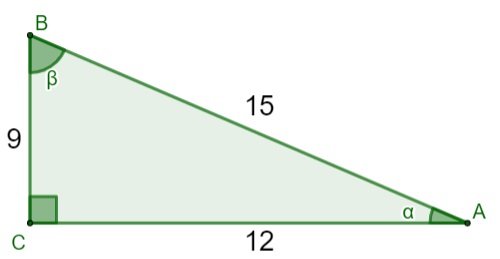
Analisando o triângulo retângulo, com suas medidas dadas em centímetros, podemos afirmar que o valor do seno do ângulo ꞵ é igual a:
 A) 3/5
B) 4/5
C) 5/4
D) 4/3
E) 3/4
A) 3/5
B) 4/5
C) 5/4
D) 4/3
E) 3/4