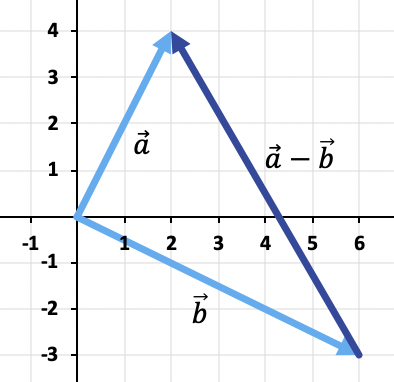
Resta de vectores
Definición.
La noción de resta de vectores se emplea en las matemáticas. En este caso, el vector es una magnitud que se grafica como un segmento que tiene su origen en un punto A y se orienta hacia su extremo (el punto B). El vector, por lo tanto, es un segmento AB.
La resta de vectores es una operación que se realiza con dos de estos segmentos. Para realizar la resta de dos vectores, lo que se hace es tomar un rector y sumarle su opuesto

Ejemplo.
Supongamos que deseamos realizar la siguiente resta: AB – DE, siendo AB (-3, 4) y DE (5, -2) de acuerdo a la posición de los vectores en el plano cartesiano. Teniendo en cuenta lo dicho sobre la suma del opuesto, deberíamos plantear la operación de este modo:
(-3, 4) – (5, -2)
(-3-5, 4+2)
(-8, 6)
Como se puede apreciar, a -3 le sumamos el opuesto de 5 (es decir, -5), mientras que a 4 le sumamos el opuesto de -2 (o sea, 2). Así, el resultado de esta resta de vectores es (-8, 6).