Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

Powers of Complex Numbers

Autor:Maremathics

DeMoivre’s Theorem

Let  be a complex number and n any integer. Then zn=(rn)(cos(n)+isin(n)) NOTE:

In calculating the powers of complex numbers, a complex number z=a+bi must be written in polar form. Then, you can find zn as the complex number

  1. whose absolute value is |z|n, the nth power of the absolute value of z,
  2. whose argument is n times the argument of z.

Geometric or exponential spiral

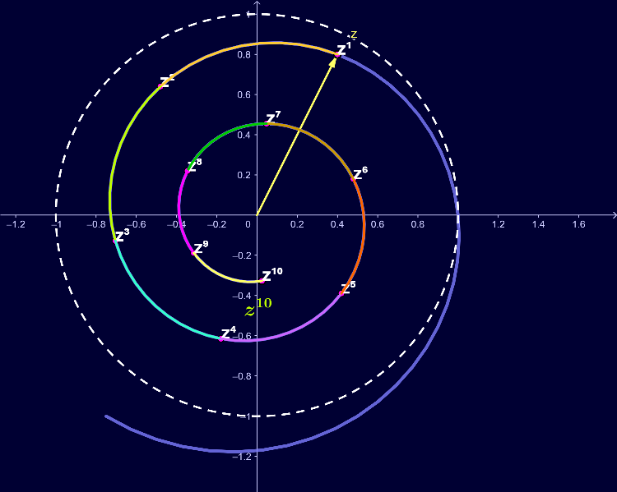
Geometric or exponential spiral
In the figure you see a complex number z whose absolute value is |z| = 0.89, and whose argument is 63.43°. Here, the unit circle is dotted white. Since |z| is less than one, it ’is within unit circle and its square is at 126.87° and closer to 0. Each higher power is 63.43° further along and even closer to 0. The first 10 powers are displayed, as you can see, as points on a spiral.
[size=100]The second figure shows the complex number z whose absolute value is |z| = 1.1, and whose argument is 84.81°. Since [b][color=#0000ff]|z| is greater than one[/color][/b], it is outside the unit circle. Each higher power is 84.81° along and [b][u]away from 0[/u][/b].[/size]
The second figure shows the complex number z whose absolute value is |z| = 1.1, and whose argument is 84.81°. Since |z| is greater than one, it is outside the unit circle. Each higher power is 84.81° along and away from 0.
Activity: The following applet you can use to show the spiral of powers. Move the sliders a and b to test for different complex numbers.

Nuevos recursos

Descubrir recursos

Descubre temas