LA ELIPSE
DEFINICIÓN
La ELIPSE es el lugar geométrico de todos los puntos del plano cuya suma de distancias a dos puntos fijos llamados FOCOS es siempre constante.

ELEMENTOS DE LA ELIPSE
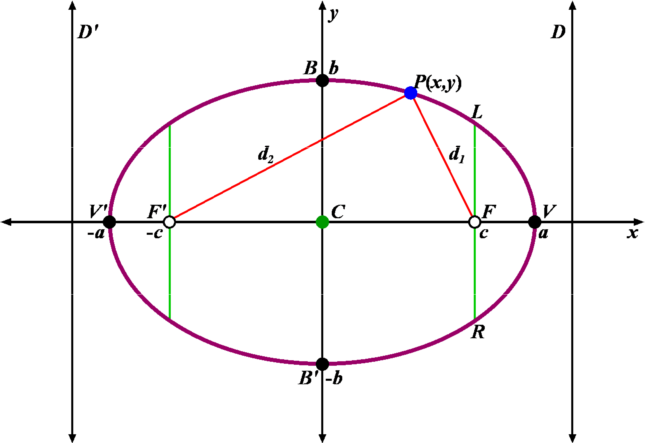



- Focos: Son los puntos fijos F
- y F'.
- Eje focal o eje de simetría: Es la recta que pasa por los focos .
- Eje normal o eje secundario: es la recta perpendicular al eje focal, y pasa por el centro, es decir, es la mediatriz del segmento
.
- Centro C: punto medio del segmento que une los focos.
- Vértices primarios: Son los puntos V y V' en que el eje focal corta a la elipse.
- Vértices secundarios: Son los puntos B y B' en que el eje normal corta a la elipse.
- Eje focal: Es el segmento de longitud
, entonces, la semieje focal es
.
- Eje mayor: Es el segmento de longitud
, entonces, el semieje mayor es
.
- Eje menor: Es el segmento de longitud
, entonces, el semieje menor es
.
- Excentricidad e: Es una cantidad constante para cada elipse, es un número que mide el mayor o menor achatamiento de la elipse. Se calcula dividiendo la longitud del semieje focal entre la longitud del semieje mayor, de la siguiente manera:
- Lado Recto (LR): Segmento de recta perpendicular al eje mayor, contiene a un foco (cualquiera de los dos) y sus extremos se localizan sobre la elipse. La longitud del lado recto se denomina ancho focal, y se calcula mediante:
- Rectas Directrices: Cada foco F de la elipse está asociado con una recta paralela al eje menor llamada directriz. La distancia de cualquier punto P de la elipse hasta el foco F es una fracción constante de la distancia perpendicular de ese punto P a la directriz.
- Radios focales: Son los segmentos
y
, determinados por un punto de la curva y los focos.
- Definición de la elipse:
(
= constante)
- Relación fundamental de la elipse:
Si el centro está en el origen (0,0) estas ecuaciones se reducen a:
- centro en el origen (0,0) y eje focal paralelo al eje x
- El centro se encuentra en el origen:
- Aclaración gráfica