Esta actividad pertenece al libro de GeoGebra Voronoi Paintings.
El preciso ajuste del diagrama de Voronoi a las siluetas del espacio positivo que se observa en los dos cuadros anteriores nos invita a realizar la siguiente pregunta: ¿hasta qué punto el diagrama de Voronoi de un cuadro devuelve información sobre las siluetas de su espacio positivo? Para intentar contestar a esta pregunta, retrocedamos al caso de sitios puntuales.
Está claro que, para cada colección de sitios, su diagrama de Voronoi es único. Ahora bien, el recíproco no tiene, en principio, por qué ser cierto. Es decir, dada una división del plano en n regiones de Voronoi puede haber más de un conjunto de n sitios que la genere.
Pensemos, por ejemplo, en cuatro sitios dispuestos en los vértices de un rectángulo. Su diagrama de Voronoi es muy sencillo: el par de mediatrices que bisecan los pares de lados opuestos del rectángulo. Ahora bien, el conjunto de cuatro sitios colocados en los vértices de cualquier otro rectángulo, con el mismo centro y lados paralelos al anterior, generará el mismo diagrama de Voronoi (Figura 21).
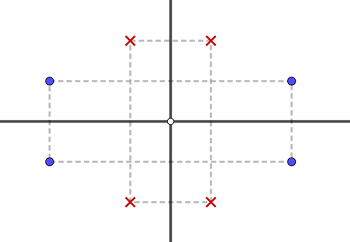
Figura 21: Los vértices de ambos rectángulos generan el mismo diagrama de Voronoi
Esto sucede porque el nodo del diagrama de Voronoi resultante, en el centro de la Figura 21 tiene grado par (4 semirrectas concurren en él), lo que permite la coincidencia en la composición de las simetrías axiales. Esto confiere cierta flexibilidad a la posición de los sitios, ver [4].
Pero recordemos que, en la práctica, podemos suponer que todos los nodos de nuestros diagramas de Voronoi tienen grado 3, con lo que la situación cambia totalmente. Efectuaremos el siguiente razonamiento para nodos de este grado, que son los que nos interesan, pero podemos generalizarlo a cualquier nodo de grado impar, ver [2].
Consideremos un diagrama de Voronoi de al menos cuatro sitios, con todos sus nodos de grado tres. Sean O y N dos nodos extremos del mismo segmento y sean A, B y C los sitios cuyo circuncentro es O (por lo que A, B y C están en posición general, es decir, no alineados), de tal modo que el segmento ON descansa en la mediatriz de A y B (Figura 22).
Para que otra terna de sitios genere el mismo diagrama, han de estar situados en triángulos homotéticos con el triángulo ABC, con centro de homotecia en O. Si ahora nos ceñimos a una sola región de Voronoi, por ejemplo, la correspondiente a A, observamos que esto fuerza a que cualquier otro sitio A’ que genere la misma región ha de situarse en la semirrecta OA. (Evidentemente, una vez fijada la posición de A’ en esa semirrecta, los otros dos sitios de la terna quedan inmediatamente determinados, pues han de ser los simétricos a A’ respecto a las aristas que concurren en O).
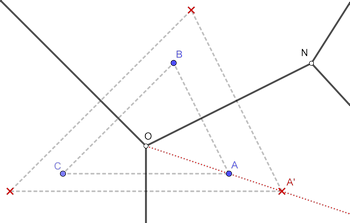
Figura 22: El sitio A’, alternativo a A, ha de situarse en la semirrecta OA
Ahora bien, aplicando el mismo argumento al nodo N, A’ ha de situarse también en la semirrecta NA. Por lo tanto, A’ ha de ser la intersección de OA y NA: A’ = A.
Concluimos entonces que, dado un diagrama de Voronoi correspondiente a n sitios puntuales (n>3), con todos sus nodos impares (es decir, prácticamente cualquier diagrama de Voronoi), ese conjunto de n sitios generador del diagrama es único.
Pasar de formas puntuales a formas circulares o poligonales no aumenta la libertad de los sitios generadores, más bien la reduce. Pensemos, por ejemplo, que una misma recta mediatriz puede ser generada por muchos pares de puntos diferentes, pero un arco parabólico determina, por sí mismo, los dos objetos de los que equidista, el foco y la directriz.
Resumiendo, cualquiera de los diagramas de Voronoi que hemos generado a partir de los cuadros determina el borde sensible de las siluetas que interviene en su generación. Como estas siluetas perfilan las zonas focales del espacio positivo del cuadro, el diagrama de Voronoi esquematiza, en un único grafo, una parte significativa de la distribución de las zonas focales en el cuadro, colaborando, así, a mejorar nuestra percepción de la forma [12].
Como reflexión final queremos señalar nuestro deseo de que el presente trabajo contribuya a destacar el valor, tanto educativo como divulgativo, que adquieren los conceptos y procedimientos matemáticos, a menudo acusados (injustamente) de fríos o áridos, al plasmarse en contextos culturales como el artístico, también a menudo declarados (justamente) como profundamente emocionales. Creemos que una educación integral es aquella que fomenta la apreciación de la belleza en cualquiera de sus formas y, a fin de cuentas, detrás de un cuadro o de un teorema siempre encontramos lo mismo: la imaginación humana.
Figura 21: Los vértices de ambos rectángulos generan el mismo diagrama de Voronoi 
Figura 22: El sitio A’, alternativo a A, ha de situarse en la semirrecta OA