Polarkoordinaten
Ein Beispiel der Polarkoordinaten.
Im Koordinatensystem können Punkte nicht nur in kartesischen Koordinaten ausgedrückt werden, sondern auch in Polarkoordinaten. Vor allem bei Radaren in der Luftfahrt werden Positionen mit Polarkoordinaten beschrieben.
Ein Punkt mit Polarkoordinaten wird mit (r;) beschrieben.
r ist eine Strecke und ist ein Winkel.
Radar
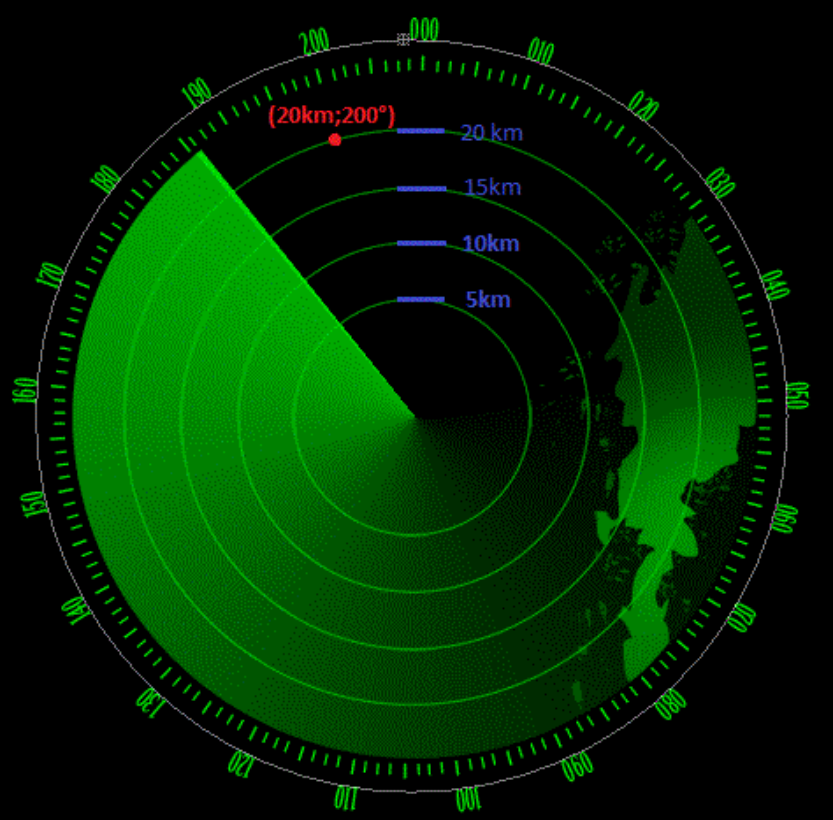
In diesem Radar sehen wir einen roten Punkt.
Dieser rote Punkt ist 20km vom Mittelpunkt entfernt und hat eine Umdrehung im Uhrzeigersinn zurückgelegt.
Es war eine Umdrehung um 200°.
Ein Beispiel im Koordinatensystem.
Nun versuchen wir zu verstehen, wie genau sich die 2 Parameter (r;) eines Punktes verhalten.
In der unteren Abbildung findest du den Punkte A, der sich nur auf der schwarzen Strecke bewegt.
Außerdem findest du noch die Punkte B;C & D, die sich nur auf den verschieden Kreisbahnen bewegen.
Alle Punkte sind verschiebbar !
Tu folgendes:
- verschiebe den Punkt A und beobachte was mit r von (r;) passiert.
Was stellst du fest ?
- verschiebe die Punkte B;C & D auf ihren jeweiligen Kreisbahnen und beobachte was mit von (r;) passiert. Was stellst du fest ?
Erschließung aus Beispiel im Koordinatensystem.
1. r von (r;) des Punktes A ist der Abstand zwischen dem Punkt a und dem Ursprungspunkt des Koordinatensystems.
2. Wird Punkt B;C oder D verschoben, ändert sich . Der Startpunkt liegt bei der X-Achse.
Verschiebt man nun zum Beispiel Punkt B von der X-Achse weiter nach links auf der roten Kreislaufbahn, steigt . ist in Grad angeben. Bewegt man den Punkt B von links nach rechts sinkt.
Der Winkel beschreibt, mit viel Grad sich ein Punkt in einer Umdrehung bewegt hat.
Bei gleicher Umdrehung ist bei allen 3 Punkten (B;C & D) gleich.
Negativer Winkel
von (r;) kann auch negativ sein.
Untersuchen wir das Ganze mit Hilfe der unteren Abbildung.
Unten findest du den Punkt B, der sich auf der Kreisbahn bewegt.
Rechts oben findest du auch einen Schieberegler mit den Intervall [-360°;360°] für .
Verschiebe den Regler und achte darauf, was mit den Punkt B passiert, wenn negative wird.
Erschließung aus Negativer Winkel.
Wenn negative wird, dann dreht sich der Punk von rechts nach links (im Uhrzeigersinn).
Bogenmaß als Winkelangabe in Polarkoordinaten.
kann auch in rad (Bogenmaß) statt ° angeben werden.
In der unteren Abbildung bewegt sich der Punkt B auf einer Kreisbahn.
Der Schieberegler und das Eingabefeld verändert von (r;) des Punktes B .
1. Nutze den Regler und das Eingabefeld um herauszufinden, wie viel 90°,180° und 360° ungefähr im Bogenmaß sind.
2. Was hat das Bogenmaß mit den Umfang eines Kreises zu tun ?
Bemerkung:
Möchtest du eine Kommazahl für den Parameter a eingeben, dann benutze einen Punkt statt ein Komma bei deiner Eingabe !!!
Die Zahlen im Schieberegler und im Eingabefeld werden noch mit Pi multipliziert.
Erschließung aus Bogenmaß als Winkelangabe in Polarkoordinaten.
Erinnerung:
Pi = 3.14159265359
Umfang eines Kreises
U = 2*r*Pi
90 ° sind 0,5*Pi.
180° sind 1*Pi.
360° sind 2*Pi.
Das Bogenmaß beschreibt den Anteil des Umfanges eines Kreises, der bereits von einem Punkt zurückgelegt wurde.
Dabei spielt der Radius der Kreisbahn, auf der sich ein Punkt bewegt, keine Rolle für das Bogenmaß.