Einführung von Vektoren
Der Vektor hat die Koordinaten:
Verschiebung durch Vektoren
Geben Sie den Vektor an, durch den das Dreieck1 auf das Dreieck2 abgebildet wird!
Wie kann man anhand von Koordinaten zweier Punkte den Vektor berechnen?
A(2/3) und B(4/1). Überlegen Sie die Lösung/Berechnung des Vektors von A nach B.
"Spitze minus Schaft" Regel
C(3/1) und D(6/5). Berechnen Sie den Vektor von C nach D.
Ortsvektor
Wenn ein Punkt die Koordinaten P(3/4) hat, dann nennt man manchmal auch den Vektor vom Ursprung zum Punkt P Ortsvektor und schreibt das so:
Betrag eines Vektor mit dem Satz des Pythagoras kann man sich die Länge (=Betrag) eines Vektors berechnen
Berechnen Sie die Länge des Vektors?
Finde einen Vektor der parallel zu ist und die Länge 1 hat.
Produkt mit einer Zahl
Probiere es im Applet darunter und ändere c und schau dir an, was mit dem Vektor passiert!Welche Vektoren sind zum Vektor parallel?
Skalarprodukt im R2
Bewege den Punkt C und schau was passiert. Was passiert wenn man die beiden Vektoren aufeinander normal stehen lässt?Berechne:
Berechne:
Winkel zwischen zwei Vektoren
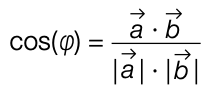
Berechne den Winkel zwischen den beiden Vektoren und
Geradengleichung in Parameterdarstellung Wir alle kennen die Geradengleichung y=kx+d, man kann eine Gerade auch mit Vektoren darstellen, man nennt das dann Parameterdarstellung. Wir haben bereits gesehen (vergleiche dazu noch einmal das bereits oben gesehene Applet) dass eine Zahl multipliziert mit einem Vektor einen Vektor ergibt der auf einen Punkt zeigt. Je nachdem wie groß wir diese Zahl c wählen, wird jeder beliebige Punkt in Verlängerung des Vektors in beiden Richtungen beschrieben.
Stelle eine Geradengleichung auf! Die Gerade geht durch den Punkt P(2/1) und ist parallel zum Vektor (1/3).
Geradengleichung:

Stelle eine Geradengleichung auf! Die Gerade geht durch den Punkt A(1/2) und durch B(3/7)