Unterrichtssequenz: Herleitung der Formel für die Berechnung des Flächeninhalts von Kreisen
Kurzinformation
Thema: Flächeninhalt des Kreises berechnen
Fach: Mathematik, Klassenstufe 9
Voraussetzungen/ Benötigtes Vorwissen:
Die Schülerinnen und Schüler sollten bis zu dieser Unterrichtseinheit ein gut fundiertes Wissen über folgende Themen haben:
(in Klammern stehen die Klassenstufen, in denen diese Themen behandelt werden)
- den Kreis / Formel für den Flächeninhalt eines Kreises (Klassenstufe 6)
- Kreiszahl (Klassenstufe 6 3,14; in Klassenstufe 9 wird mit der Berechnung des Umfangs
auch die Kreiszahl als irrationale Zahl eingeführt)
- Flächeninhaltsberechnung von Dreiecken/ Rechtecken (Klassenstufen 6)
- Kongruenz von Dreiecken (Klassenstufe 9)
- Seitenverhältnisse im rechtwinkligen Dreieck (Klassenstufe 9)
Ziel der Unterrichtssequenz
Die Berechnung des Flächeninhalts eines Kreises wird in der sechsten und neunten Klassenstufe behandelt.
In der sechsten Klassenstufe wird die Formel für den Flächeninhalt eines Kreises sehr einfach hergeleitet.
In der Klassenstufe 6:
Man nähert sich der Fläche eines Kreises mit Radius r, indem man in den Kreis ein Viereck, dessen Seiten gleich lang sind – also ein Quadrat – so hineinzeichnet, dass alle Eckpunkte auf dem Kreis liegen.
Der Flächeninhalt dieses einbeschriebenen Quadrats beträgt 2r2.
Zusätzlich umschreibt man den Kreis mit Radius r mit einem Quadrat mit der Seitenlänge 2r.
Der Flächeninhalt des umschreibenden Quadrats beträgt 4r2.
Der Lambacher Schweizer an dieser Stelle: „Der Flächeninhalt des Kreises liegt somit zwischen 2r2 und 4r2. Man kann zeigen: A = · r2 3,14 · r2 ".
Ziel dieser, für die neunte Klassenstufe konzipierte Unterrichtssequenz, ist es, die in der sechsten Klassenstufe mehr oder weniger „stiefmütterlich“ behandelte Formel für die Berechnung des Flächeninhalts des Kreises herzuleiten.
Diese Herleitung wird mithilfe eines Grenzprozesses bestimmt – somit wird man dem Bildungsplan diesbezüglich gerecht.
Ablauf der Unterrichtssequenz
1. Einführung und Wiederholung
Man beginnt die Stunde mit dem Bild eines Wohnhauses mit kreisförmiger Grundfläche (siehe "Wohnhaus mit kreisförmiger Grundfläche").
Die Berechnung des Flächeninhalts des Wohnhauses mit einer kreisförmigen Grundfläche sollte in der neunten Klassenstufe eigentlich kein Problem sein.
Also fragt man die Schülerinnen und Schüler nach der Formel für die Berechnung des Kreises.
Kommt dann wieder zurück auf die Art und Weise, wie diese Formel in der Klassenstufe 6 erarbeitet wurde (siehe "Flächeninhalt des Kreises in Klassenstufe 6") und weist darauf hin, dass diese „Herleitung“ für den heutigen Wissensstand der Schüler und Schülerinnen nicht zufrieden stellend ist.
So erfrischt man das Vorwissen der Schülerinnen und Schüler und kann dort anknüpfen und darauf aufbauen.
2. Erarbeitung der Formel für die Berechnung des Flächeninhalts des Kreises (in Plenum)
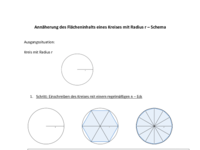
"Annäherung des Flächeninhalts eines Kreises mit Radius r - Schema.pdf" wird den Schülern
und Schülerinnen ausgehändigt. So wird ihnen klar, wie der Grenzwert - Prozess, mit dem man
sich dem Flächeninhalt des Kreises mit Radius r annähert, aussieht.
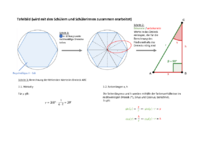
Wie der Flächeninhalt eines regelmäßigen n - Ecks berechnet wird, wird dann an der Tafel
exemplarisch an einem regelmäßigen 6 - Eck zusammen mit den Schülern und Schülerinnen
erarbeitet. (Siehe Tafelbild zur Unterrichtssequenz)
Hinweise zum verwendeten GeoGebra - Applet
Das verlinkte GeoGebra – Applet ermöglicht es die Approximation zu veranschaulichen, und
sie so für die Schüler und Schülerinnen ersichtlich und verständlich zu machen.
Das Applet nimmt der Lehrkraft sehr viel Arbeit ab, da schon ab einem „kleinen“ n die Tafel als
Medium zur Veranschaulichung der Approximation versagt.
Zudem stellt das Nutzen des Applets eine Zeitersparnis dar, da man sehr viel mehr Zeit
bräuchte, um die Approximation eigenhändig an der Tafel vorzuführen.
Außerdem ist das Applet von Schülern und Schülerinnen immer aufrufbar.
Wohnhaus mit kreisförmiger Grundfläche
Flächeninhalt eines Kreises in Klassenstufe 6
Annäherung des Flächeninhalts eines Kreises mit Radius r - Schema
Tafelbild zur Unterrichtssequenz
GeoGebra - Applet (Beachte Flächeninhalt anstatt Fläche)
Didaktischer Hintergrund: Spiralprinzip
Das Spiralprinzip ist als Grundlage für die Unterrichtsplanung in der Mathematikdidaktik weitgehend unumstritten.
Dieses geht auf den US- amerikanischen Psychologen Jérôme Seymour Bruner zurück, der es in seinem Buch "The Process of Education“ beschreibt (vgl. Büchter, 2014).
Bruners Ausgangspunkt bei der Entwicklung des Prinzips war folgende Hypothese:
„Jedem Kind kann auf jeder Entwicklungsstufe jeder Lehrgegenstand in einer intellektuell ehrlichen Form erfolgreich gelehrt werden„ (Bruner, 1973).
Intellektuelle Ehrlichkeit ist hierbei als „vereinfachen, ohne zu verfälschen“ zu verstehen. Er stellt die Betrachtungsweise von Kindern folgendermaßen dar:
„das Kind [hat] auf jeder Entwicklungsstufe eine charakteristische Art und Weise [ ], die Welt zu betrachten und für sich selbst zu erklären. Ein Kind bestimmten Alters in einem Lehrgegenstand zu unterrichten bedeutet, die Struktur dieses Gegenstandes in der Art und Weise darzustellen, wie das Kind Dinge betrachtet“ (Bruner 1973, S. 44).
Genau dieses Prinzip liegt der oben dargestellten Unterrichtseinheit zugrunde.
In der sechsten Klassenstufe wird die Formel für die Berechnung des Flächeninhalts eingeführt. Dabei wird die Herleitung nur sehr mager behandelt, da das Vorwissen der Schüler und Schülerinnen nicht für eine ausführlichere Herleitung reicht. Mit der Behandlung dieses mathematischen Themas bis zu einem bestimmten Vollständigkeitsgrad schafft man jedoch ein Fundament, auf das man zu einem späteren Punkt in der Schullaufbahn aufbauen kann (vgl. Lauter 1997, S.52).
In der neunten Klassenstufe, nachdem Kongruenz von Dreiecken und die in einem rechtwinkligen Dreieck herrschenden Seitenverhältnisse gelehrt wurden, wird die Formel für die Berechnung des Flächeninhalts eines Kreises, zum einen „auf einem höheren Niveau“ (Demirezen, n.d.) und zum anderen in einer “strukturell angereicherte[n] Form“(Demirezen, n.d.), nochmal aufgegriffen. So wird die bewusst offen gelassene Lücke geschlossen.
Bei der Herleitung der Formel für den Flächeninhalt eines Kreises auf dem Niveau der neunten Klassenstufe liegt es nahe, sich und den Schülern und Schülerinnen mit einem GeoGebra – Applet weiterzuhelfen. So wird die Approximation visualisiert und der Sachverhalt für jeden ersichtlich und verständlich gemacht.
Literaturverzeichnis / Abbildungsverzeichnis
Literaturverzeichnis
Bruner, J. S. (1973): Der Prozeß der Erziehung (3. Aufl.). Berlin: Berlin Verlag.
Büchter, A. (2014). Das Spiralprinzip. mathematiklehren, 2014(182), 2f.
Buck, H. et al. (2015). Lambacher Schweizer 6. Mathematik für Gymnasien (1. Auflage). Ernst Klett Verlag.
Demirezen, N. & Güner, G. (n.d.). Spiralprinzip. Retrieved December 01, 2022, from https://kira.dzlm.de/kirafiles/uploads/doc/Spiralprinzip.pdf
Freudigmann, H. et al. (2018). Lambacher Schweizer 9. Mathematik für Gymnasien (1. Auflage). Ernst Klett Verlag.
Lauter, J. (1997): Fundament der Grundschulmathematik. Pädagogisch-didaktische Aspekte des Mathematikunterrichts in der Grundschule (3. Aufl.). Donauwörth: Auer.
Abbildungsverzeichnis
Abbildung 1: Wohnhaus mit kreisförmiger Grundfläche
https://www.radius-design.com/images/content/AbsolutGrundriss-EG.png, 01.12.2022
Abbildung 2: Flächeninhalt eines Kreises in Klassenstufe 6
Buck, H. et al. (2015). Lambacher Schweizer 6. Mathematik für Gymnasien (1. Auflage). Ernst Klett Verlag.