Optische Länge des gebrochenen Lichtwegs
Hintergrund
Zuvor wurde die geradlinige Lichtausbreitung und das Reflexionsgesetz aufgegriffen und vor dem Hintergrund des Fermatschen Prinzips modelliert. Es wird genutzt, um eine Vorhersage bezüglich des Verhaltens von Licht beim Übergang von einem transparenten Medium (z. B. Luft) in ein anderes (z. B. Wasser oder Acrylglas) abzuleiten.Der geometrisch kürzeste Lichtweg würde auf der geraden Verbindung zwischen Q in einem Medium und E in einem anderen Medium liegen. Allerdings kann es Gründe geben, von dem kürzesten Weg abzuweichen:
Eine Person, die eine andere aus dem Wasser retten möchte, ist auf dem Land schneller ist als im Wasser. Der am Ufer zurückgelegte Weg ist deshalb intuitiv etwas länger als die restliche Strecke im Wasser. In der Summe führt diese Taktik schneller ans Ziel als der direkte Weg.
Wird von unterschiedlichen Werten für die Lichtgeschwindigkeit c in unterschiedlichen Medien ausgegangen, bietet es sich an, diese Idee auf das Verhalten von Licht an Grenzflächen zu übertragen. Dieser Sachverhalt wird mit dem Brechungsindex definiert, wobei c0 für die Lichtgeschwindigkeit im Vakuum steht.
Damit lässt sich die optische Weglänge eingeführt, wobei s für die geometrische Länge des Lichtwegs steht.
Modell
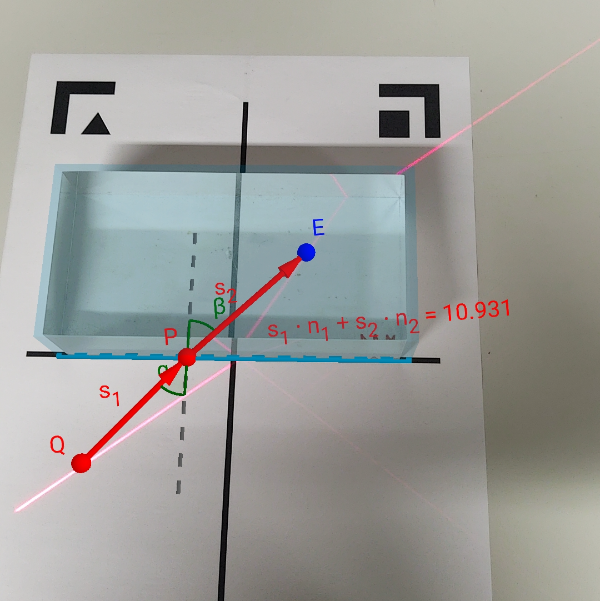
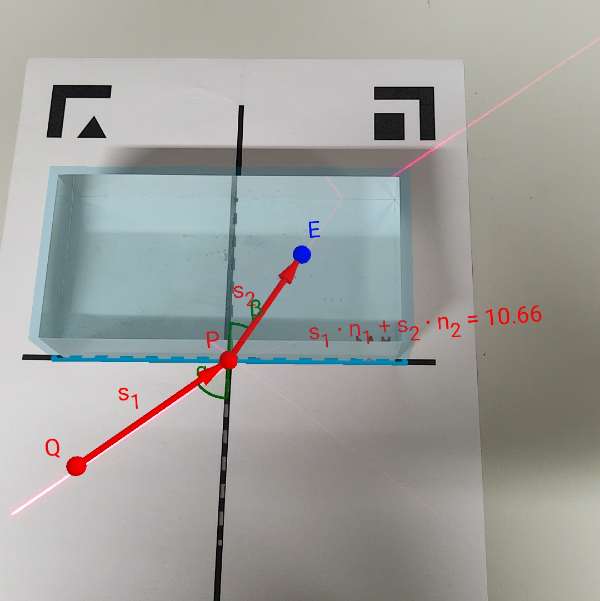
Mithilfe des Fermatschen Prinzips lassen sich verschiedene Lichtwege zwischen Q und E über den Punkt P vergleichen, der sich auf der Grenzfläche zwischen zwei
Medien mit den Brechungsindizes n1 und n2 befindet. Statt der üblichen Summe werden die optischen Weglängen der beiden Abschnitte aufsummiert und für jede Position von P ausgegeben.
Verschiebe mit dem Schieberegler P auf der Grenzfläche, bis der Wert minimal wird.
Hypothese
Brechungsgesetz
Für einen Lichtweg mit der kürzesten Laufzeit (OWL minimal) gilt das vereinfachte Brechungsgesetz:
Experiment
Inwiefern das mit der optischen Weglänge verfeinerte Fermatsche Prinzip die Lichtbrechung vorhersagt, lässt sich im Experiment mit einem Linienlaser und einem Quader aus Acrylglas zeigen. Im Modell müssen dafür die Brechungsindizes für Luft als n1 = 1 und für das im Experiment verwendete Acrylglas als n2 = 1,49 eingestellt werden. In AR werden zunächst die Punkte Q und E entlang der realen Leuchtspur ausgerichtet. Danach kann gezeigt werden, dass die optische Weglänge genau dann minimal wird, wenn P an die Stelle geschoben wird, an der das Licht die Grenzfläche trifft und der Lichtweg einen Knick macht.