GeoGebra

summary

Auteur :Walter Füchte

Hommage an Walter Wunderlich

Hommage an Walter Wunderlich
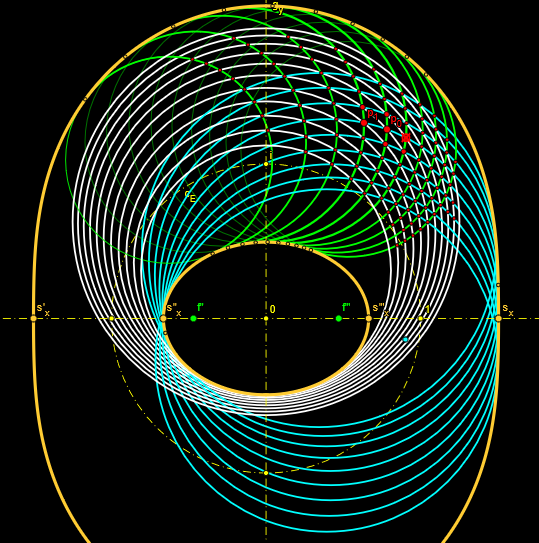
geogebra-book elliptische-Funktionen&&Kreisbüschel&&bizirkulare-Quartiken&&6-Eck-Netze-aus-Kreisen Link https://www.geogebra.org/m/nzfg796n Elliptische Funktionen lassen sich charakterisieren durch eine elliptische Differential-Gleichung des Typs
  • mit komplexen
Für die WEIERSTRASSsche -Funktion ist einer der 4 Brennpunkte . Kreisbüschel werden beschrieben durch eine Differentialgleichung mit geeignetem . Eine Elliptische Funktion ist auf mehrfache Weise das Produkt zweier Kreisbüschel, Lösungskurven sind dann Winkelhalbierende der Kreise aus den 2 Büscheln. 4 verschiedene ("Brenn")-Punkte lassen sich durch eine geeignete Möbiustransformation abbilden auf mit komplexem . Ist die absolute Invariante der 4 Brennpunkte -d.i. auch die absolute Invariante der elliptischen Differentialgleichung - reell, so sind konfokale bizirkulare Quartiken Lösungskurven: 2-teilige für , 1-teilige für . Für gilt beides: die 1-teiligen schneiden die 2-teiligen unter 45°: harmonische Lage der Brennpunkte. Tetraederlage: , zu jeder Paarbildung der Brennpunkte sind konfokale 1-teilige Quartiken Lösungskurven; sie schneiden sich unter Vielfachen von 30°. Die Brennpunkte sind - auf der Möbiusquadrik - die Ecken eines regulärenTetraeders. Die Eigenschaften konfokaler bizirkularer Quartiken sind mindestens so faszinierend wie die der konfokalen Kegelschnitte, welche möbiusgeometrisch eigentlich nur Spezialfälle sind: von den 4 Brennpunkten fallen 2 oder 3 zusammen! Geometrisch lassen sich bizirkulare Quartiken durch ihre Brennpunkte, ihre Leitkreise und die doppelt-berührenden Kreise als Hüllkurven beschreiben. Obwohl zu diesen Quartiken einige spezielle bekannte historische Kurven gehören, hat diese Kurvenklasse noch keinen Einzug in wikipedia gehalten. Mindestens ebenso faszinierend sind die 3-dimensionalen Pendants: die konfokalen DARBOUX Cycliden, zu denen auch die konfokalen Quadriken gehören. geogebra-book conics bicircular-quartics Darboux-cyclides https://www.geogebra.org/m/gz4cyje5 W. Blaschke stellte 1938 die Frage nach allen 6-Eck-Geweben aus Kreisen. Gelöst war zu der Zeit die Frage nach allen geradlinigen 6-Eck-Geweben: Satz von Graf und Sauer: diese Gewebe entstehen aus den Tangenten einer Kurve 3. Klasse. Kurioser Weise ist Blaschkes Problem 3D für Kreise auf Flächen gelöst: nur auf DARBOUX Cycliden existieren solche Kreis-Gewebe; und sie sind alle erfaßt! Einzige Ausnahme: für Kreise auf Ebenen oder Kugeln ist Blaschkes Problem weiter ungelöst! Ein wunderschöner Referenzartikel zu allen bisher bekannten ebenen 6-Eck-Geweben aus Kreisen ist Walter Wunderlichs Arbeit von 1938 "Über ein besonderes Dreiecksnetz aus Kreisen": 2-teilige bizirkulare Quartiken besitzen 4 paarweise orthogonale Symmetriekreise und dazu 4 Scharen doppelt-berührender Kreise. Aus drei dieser Scharen läßt sich ein 6-Eck-Gewebe erzeugen. 2013 veröffentlichte Fjodor Nilov 5 bis dahin unbekannte 6-Eck-Gewebe aus Kreisen, zugrunde liegen allen Beispielen spezielle Kegelschnitte. Wir konnten 4 der Beispiele verallgemeinern zu eine Reihe von bisher unbekannten 6-Eck-Geweben, die bizirkulare Quartiken zugrunde legen. Wie rechnet man so etwas? Leider ist ein gut passender spezieller Kalkül für Kreise uns nicht zugeflogen. Für Kreisbüschel jedoch gibt es einen einfachen, genau passenden Kalkül: Die ebene Möbius-Gruppe ist isomorph zur komplexen . (Vor vielen Jahren fand man diese sehr nützliche Repräsentation noch auf wikipedia - dort ist sie schon lange verschwunden!?) Die LIE-Algebra hierzu ist die Komplexifizierung des Euklidischen Vektorraums: das Kreuzprodukt wird zum LIE-Produkt, das Skalarprodukt wird zu einer symmetrischen nicht-ausgearteten und natürlich nicht mehr positiv-definiten Bilinearform. Die Punkte (Vektoren) auf der entstehenden Quadrik lassen sich als parabolische Kreisbüschel deuten, die anderen Punkte gehören zu elliptischen/hyperbolischen Kreisbüscheln und deren Isogonaltrajektorien (Loxadrome). Deuten lassen sich die Vektoren als Infinitesimale Möbiustransformationen. Multiplikation mit ist die Polarität. Die Orthogonalität und die LAGRANGEsche Entwicklungsregel lassen sich nutzen. Beispielsweise läßt sich damit die Lage von 4 Punkten (in einfach charakterisieren. Links: geogebra-book Sechseck-Netze https://www.geogebra.org/m/z8SGNzgV geogebra-book Möbiusebene https://www.geogebra.org/m/kCxvMbHb

summary – GeoGebra

summary – GeoGebra.pdf

summary – GeoGebra.pdf

Nouvelles ressources

Découvrir des ressources

Découvrir des Thèmes