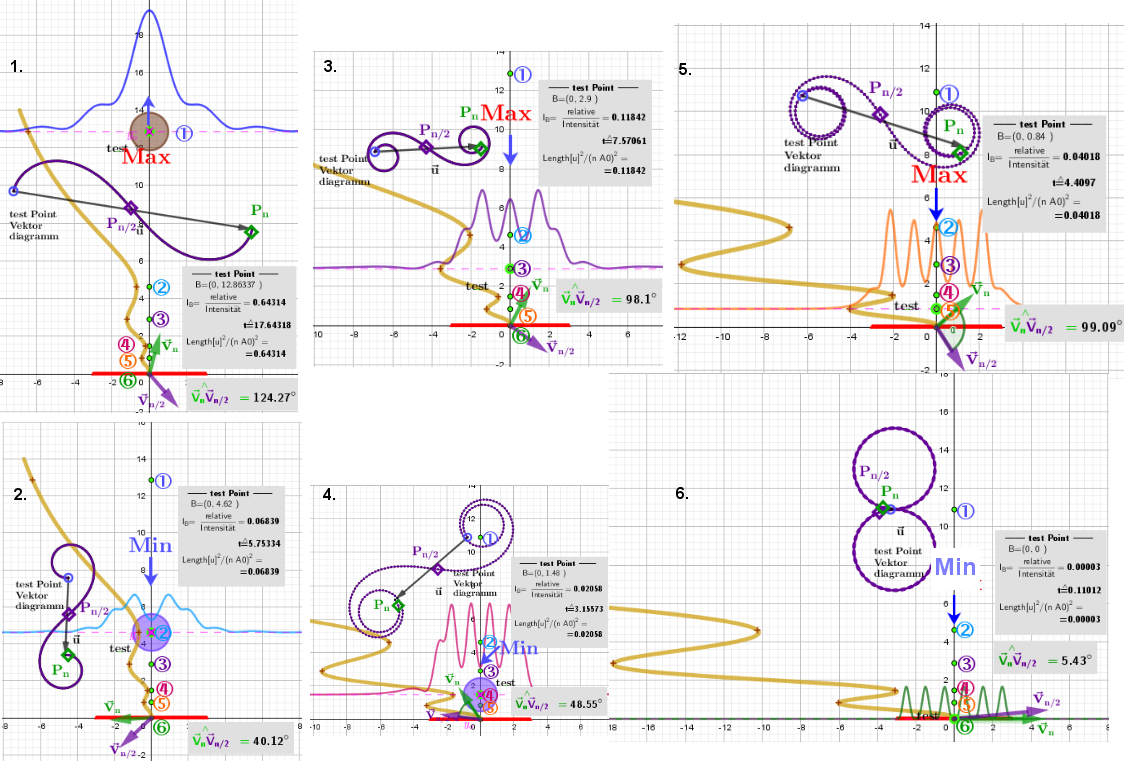
Veranschaulichung der Änderung des Vektordiagramms der Schwingung des resultierenden Feldes für Punkte auf der Achse des Spaltes.
Der Zweck des Applets besteht darin, die Struktur der Nahfeldinterferenz/Beugung (-Nahfeld (Fresnel-Beugung),"Talbot-Teppich" sieh an: Talbot effect und Artikel) einer endlichen Anzahl von ungedämpften Wellen aus äquidistanten Quellen, die sich in einem engen Spalt befinden, zu veranschaulichen. Die Konstruktion von Zonen erfolgt in einem Fall analog zu kreisförmigen Fresnel-Zonen. Es ist jedoch zu beachten, dass die Anzahl der Quellen für den betrachteten Fall in den verschiedenen Zonen unterschiedlich ist! Bei einem anderen Verfahren sind die Brennpunkte die Extrema der Strahlungsintensitätsverteilungskurve entlang der Spaltachse sein.
Hier wird der Vergleich von zwei Fällen von Vektordiagrammen für Punkte auf der Spaltachse untersucht.
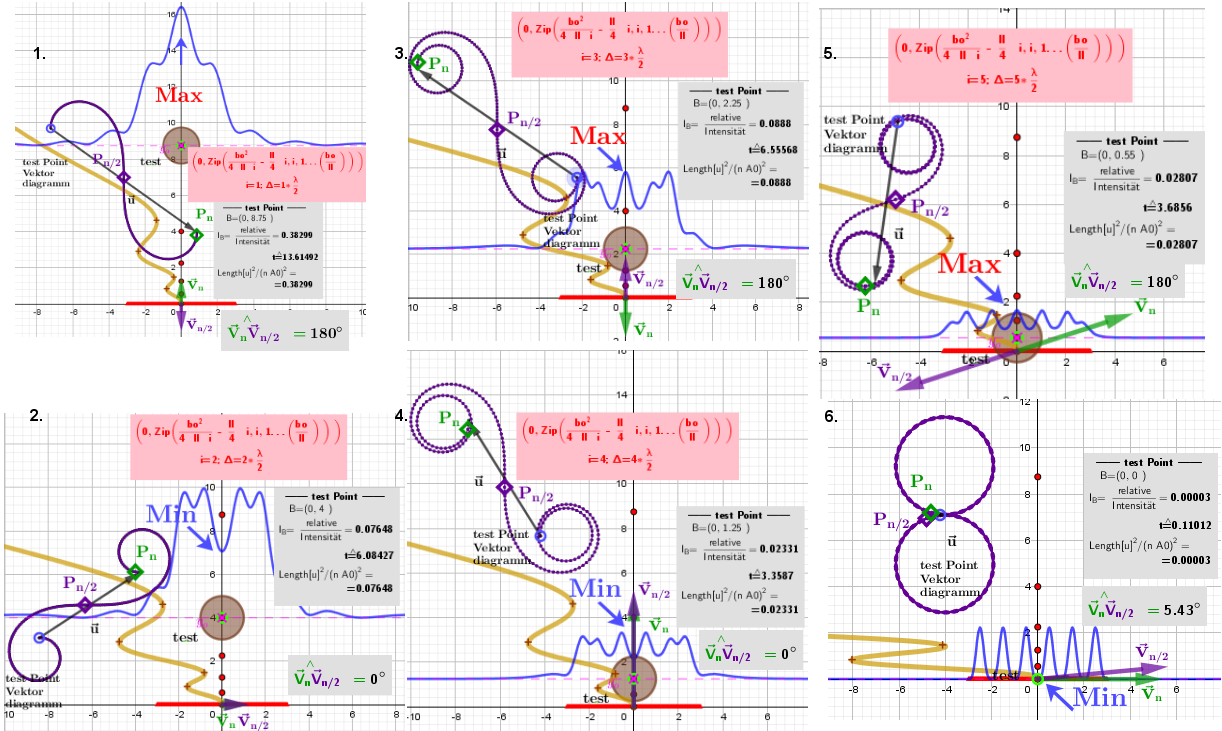
Im ersten Fall werden die Punkte ausgewählt, die den formal "Brennpunkten der Fresnel-Zonen"entsprechen. Geometrisch entspricht dies den Fällen, in denen die Gangunterschied zwischen dem Mittelstrahl und dem Strahl von der Spalt-Kante ein Vielfaches von λ / 2 ist. Pₙ-der Punkt im Vektordiagramm, der dem Strahl vom Rand des Spaltes entspricht, Pn/2 entspricht dem Strahl entlang der Achse des Spaltes. Die Phasendifferenz der Schwingungen von diesen Punkten ist 180°.
Im zweiten Fall entsprechen die "Brennpunkte der Fresnel-Zonen" den Extremen der Intensitätskurve entlang der Spaltachse. Beachten Sie in diesen "Brennpunkten" die horizontale Intensitätsverteilung haben jeweils 1,2,3,...,⌊b/λ⌋ Peaks of Intensität. Die Position des ersten Peaks ist nicht definiert, da die Wellen sich ohne Dämpfung ausbreiten. Hier wird dieser Punkt zufällig ausgewählt.
Der Fall, wenn der Gangunterschied zwischen dem Strahl, der sich entlang der Achse des Spaltes und vom Rand des Spaltes ausbreitet, ein Vielfaches von λ / 2 ist.
Der Fall, wenn die "Brennpunkte der Fresnel-Zonen" den Extrempunkten der Intensitätskurve entlang der Spaltachsen entsprechen.