1.2. Funciones lineales
Funciones lineales
Para entender el concepto de "función lineal" hay que tener en cuenta y comprender, varios conceptos. Función En las funciones hay unos elementos de entrada, hay una función (proceso), y una salida o resultado. Diremos que una función es una relación entre dos o más variables . Las funciones constituyen una herramienta útil para describir, analizar e interpretar diferentes situaciones provenientes de la Matemática y otras ciencias. Variables Al hablar de variables, nos referimos a los diferentes elementos, factores, características que definen un objeto, una situación o un fenómeno. Ejemplo: el peso, la cantidad, la velocidad, el tiempo, el color, la altura, etc. En matemática (lógica, estadística, economía y otras ciencias) una variable es un símbolo (generalmente una letra) que representa un valor o elemento desconocido. Por ejemplo: Para representar "cualquier" número se puede representar por X, o cualquier letra, y en una ecuación como puede ser 2x-7, la X representa la variable. Tipos de variables: En una función tenemos dos tipos de variables: Independiente y Dependiente. La variable Independiente, como su nombre lo indica, no depende de nadie, es la que incide en el valor o desempeño de la otra con la que se relaciona. Generalmente se denota con la letra X, y en el plano cartesiano corresponde al eje horizontal o de abscisas. La variable Dependiente, depende de la variable independiente, es decir, su valor o comportamiento está determinado por los valores que tome X. Generalmente se denota con la letra Y, y en el plano cartesiano corresponde al eje vertical o de ordenadas. Ejemplos:
- En la relación entre el precio que se paga por un producto y la cantidad comprada; la cantidad (variable x) determina el precio a pagar (variable y)
- En la relación, velocidad y tiempo, la velocidad (variable x) determina el tiempo gastado en recorrer una distancia cualquiera (variable y)
Relación entre variables El tipo de relación entre las variables en una función es proporcional, es decir, que aumentan o disminuyen en la misma proporción. De acuerdo a esto, la relación entre las variables puede ser "directamente proporcional" o "inversamente proporcional". Directamente proporcional: cuando una variable aumenta o disminuye, la otra también aumenta o disminuye en la misma proporción. Ejemplo: la cantidad de pan (en kilos) y su precio. A mayor cantidad, mayor precio pagado y viceversa. Inversamente proporcional: cuando una variable aumenta la otra disminuye y viceversa, en la misma proporción. Ejemplo: la velocidad a la que va un auto y el tiempo que tarda en recorrer una distancia. A mayor velocidad, menor tiempo y viceversa. LA FUNCIÓN LINEAL La función lineal es la representación de la relación entre dos variables. Esta representación la podemos realizar a través de un enunciado de una situación problemática, una fórmula matemática o de una gráfica en el plano cartesiano.
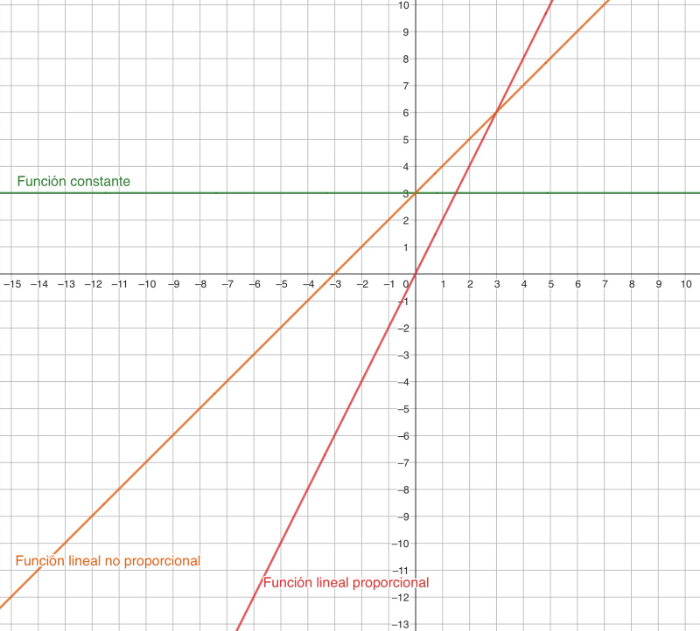
La gráfica resultante va a ser una línea recta. Su fórmula general es: f(x)= mx + n o, y = mx + n (Función lineal no proporcional: no pasa por el origen, corta al eje Y en n) donde:
m = es la pendiente de la recta, es decir si inclinación. si m > 0 (positiva) la recta va es creciente. Si m < 0 (negativa) la recta va es decreciente y si m = 0, la recta es constante n = es la ordenada en el origen, o sea donde la recta corta al eje Y (cuando la recta NO pasa por el origen) y como vemos en la ecuación de recta, n, corresponde al término independiente (número que no está acompañado de letras) Si se tienen dos puntos (coordenadas) y a partir de ellos encontrar la formula de la recta para hallar la pendiente, o sea la variación en Y sobre la variación en X.
Además, existen los siguientes casos particulares para la función de la recta:
f(x)=y= mx (Función lineal proporcional: pasa por el origen (coordenada (0,0), no tiene variable independiente)
f(x)=y=n (Función constante)