Spherical Coordinates
Task
Create an applet to observe the motion of a point on a sphere when changing its spherical coordinates.
Explore the construction...
Instructions
| 1. |  | Activate the Sphere with Center through Point tool from the 3D Graphics View Toolbar. Click on the points (0, 0, 0) and (0, 0, 1) to create a sphere. |
| 2. | 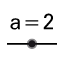 | Select the Slider tool from the Graphics View Toolbar and create a slider for angle . Use the default settings for sliders and select Apply. |
| 3. | 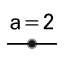 | Click in the  Graphics View again to create a second slider with default settings.
|
| 4. |  | Enter r = 1 into the Input Bar.
|
| 5. | | Enter the conversion of spherical coordinates for point P into the Input Bar: |
| 6. | | Enter the point P = (X, Y, Z) into the Input Bar.
|
| 7. | | Enter Segment((0, 0, 0), P)
into the Input Bar to create a segment between the point of origin to the point P.
|
| 8. |  | Enhance your construction using the Style Bar. |
| 9. |  | Activate the Move tool and explore the motion of the point P by dragging the sliders. |
Try it yourself...
Coordinate numbers of points in the 3D drawing window
Just like in the 2D drawing window, you can define the individual coordinate numbers of a point P as a separate number in the 3D drawing window.
- The cartesian coordinates of a point P are determined as (x(P), y(P), z(P)). With x(P), y(P), z(P) you create separate numbers for the coordinates of point P.
- spherical coordinates: P is determined as (abs(P), arg(P), alt(P)).