CircularArcDifferentialProjection
The circle quadratic equation
x2 + y2 = r2 = const [1]
means that the sum of two variable areas x2 and y2 equals the constant area r2. Here we will show what these areas look like. Taking differential of that quadratic equation, we have the differential equationx⋅dx + y⋅dy = 0 [2].
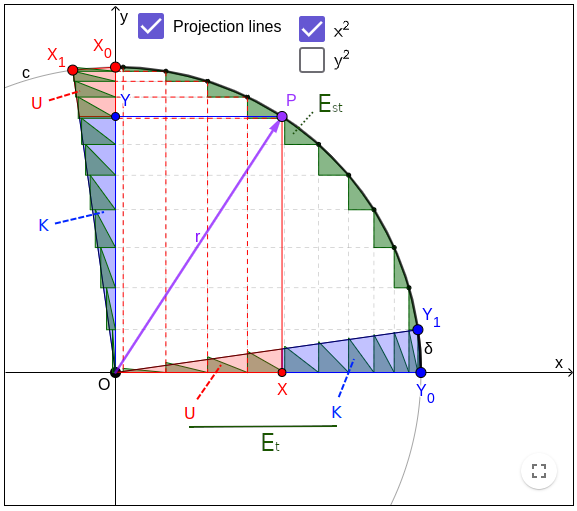
This differential equation gives us a tool to project the differentials of the quarter arc OY0X0 onto x-axis and y-axis, where each image is a differential sector swept by r along a differential arc δ as well as along a differential angle dφ = δ/r, as shown by Projection lines (in the applet above). That means the circular area ∫dx⋅dy along OY0X0 equals to the linear area ½r⋅δ of each differential sector which corresponds to the constant r2 via ½r⋅δ = ½r2(δ/r) = ½r2dφ. The quarter arc OY0X0 is split by r into two arcs OY0P and OPX0 whose images on axes correspond to y2 and x2, respectively, with areas ½y2dφ and ½x2dφ.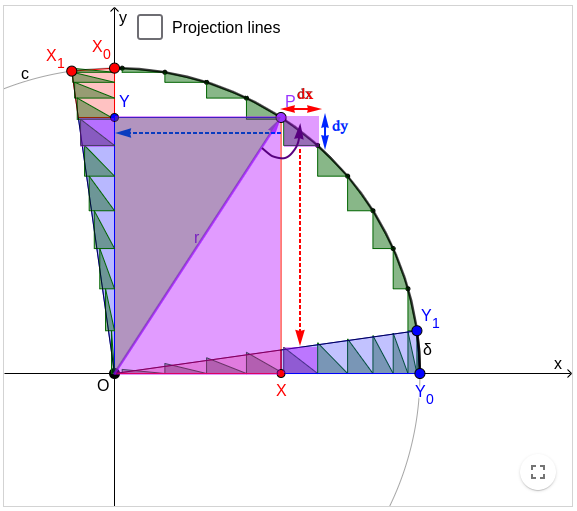
The eq.[2] means the differential tangent vector dr = (dx, dy) is orthogonal to the radius vector r = (x, y), because their scalar product is zero. By choosing an arbitrarily small value δ = |dr| to set the length of all differential tangent vectors, eq.[2] also means that the radius rectangle OXPY = [x, y] can be rotated 90° and scaled down a factor δ/r to become the differential tangent rectangle [-dx, dy]:
x(-dx) = y⋅dy [2'], [3], [4].
Then we can translate the differential tangent rectangle [-dx, dy] to x-axis and to y-axis; Applying eq.[4] we have:[5];
- On x-axis: The area of the differential quarter arc OY0X0 is the area of the differential sector OY0Y1.
- On y-axis: The area of the differential quarter arc OY0X0 is the area of the differential sector OX0X1.
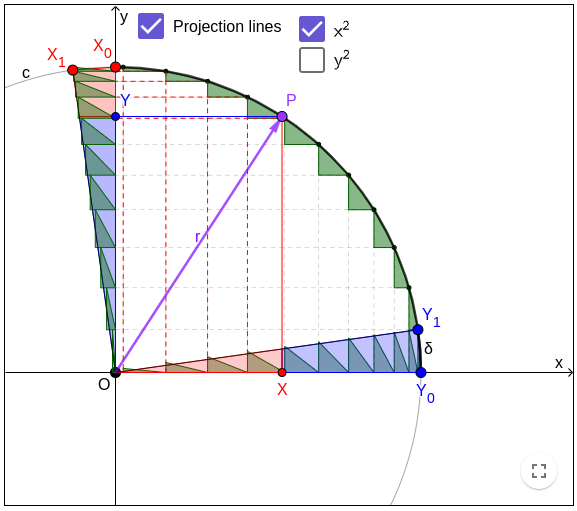
The circular area ∫dx⋅dy along the arc OY0X0 is split by r (P) into two arcs OY0P and OPX0,
The images of P on x-axis and y-axis also split differential sectors into (differential) top triangles and (differential) bottom trapezoids, which correspond to the two arcs OY0P and OPX0:
- The y2 part as shown by Projection lines > y2: The area along arc OY0P = top triangle on y-axis OYY' (y2) = bottom trapezoid on x-axis XY0Y1X' (r2 - x2).
- The x2 part as shown by Projection lines > x2: The area along arc OPX0 = top triangle on x-axis OXX' (x2) = bottom trapezoid on y-axis XX0X1Y' (r2 - y2).
Spiral on the flat cone & phase space
The result of differential projection of the quarter arc OY0X0 onto axes is sawtooth waveforms in the differential sectors. Considering the sectors as flat cones, whose two edges of r are identical ("wrapped around" like in the flat torus), those sawtooth waveforms become conical spirals.
When the Oxy plane is a position-momentum phase space, the flat cone of x-axis shows the wrapped-around total space of that phase space preserving the full momentum (velocity) vectors, whereas the momentum (velocity) vectors on x-axis are just collapsed (projected) image of these vectors.
Dynamics
The circle can be viewed a phase portrait of a simple harmonic oscillator
; .
There, x-coordinate is the position s and y-coordinate is the scaled momentum; ;
The differential phase dφ = δ/r = ωdt sweeps a differential sector A = ½r2dφ corresponding to time-differential energy
and the differential tangent rectangle a[-dx, dy] corresponds to spacetime-differential energy
The current position P splits the time-differential energy Et into two components: potential energy U ~ x2 and kinetic K ~ y2.;
When ω = 1, we have simple formulae: x = s = r cos(t); y = v = -r sin(t).