Google Classroom
GeoGebraClasse GeoGebra
GeoGebra

Completing the Square and Area

Auteur :Ethan Wright, Integral Resources
Use the slider bars to set the values of then in the equation . How do you know that the blue regions in each diagram have equal area? How do you know that the shape on the right is square? How do you find the area of the yellow region? Why is this process called COMPLETING THE SQUARE? How is the process of completing the square helpful to solve the equation? Use this applet to help answer the question: What is another way to write ?

1.

Optima has a quilt shop where she sells many colorful quilt blocks for people who want to make their own quilts. She has quilt designs that are made so that they can be sized to fit any bed. She bases her designs on quilt squares that can vary in size, so she calls the length of the side for the basic square x, and the area of the basic square is the function . In this way she can customize the designs by making bigger squares or smaller squares. If Optima adds 3 inches to the side of the square, what is the area of the square?

When Optima draws a pattern for the square in problem #1, it looks like this

When Optima draws a pattern for the square in problem #1, it looks like this

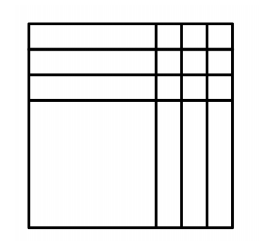
2.

Use both the diagram and the equation, to explain why the area of the quilt block, is also equal to .

The customer service representatives at Optima's shop work with customer orders and write up the orders based on the area of the fabric needed for the order. As you can see from problem #2 there are two ways that customers can call in and describe the area of the quilt block. One way describes the length of the sides of the block and the other way describes the area of each of the four sections of the block. For each of the following quilt blocks, use the interactive technology to create the diagram of the block and write two equivalent equations for the area of the block.

3.

Block with side length: x+2

4.

Block with side length: x+1

5. What patterns do you notice when you relate the diagrams to the two expressions for the area?

6.

Optima likes to haver her little dog, Clementine, around the shop. One day the dog got a little hungry and started to chew up the orders. When Optima found the orders, one of them was so chewed up that there were only partial expressions for the area remaining. Help Optima by completing each of the following expressions for the area so that they describe a perfect square. Then, write the two equivalent equations for the area of the square. Use the applet to help you get a visual representation of what is occurring mathematically .

a.

b.

c.

d.

7.

If is a perfect square, what is the relationship between b and c? How do you use b to find c, like in problem 6? Will this strategy work if is negative? Why or why not? Will the strategy work if is an odd number? What happens to if is odd?

Nouvelles ressources

Découvrir des ressources

Découvrir des Thèmes