Google Classroom
GeoGebraTarefa
GeoGebra

Circunferência e ângulos na circunferência

Autor:Lurdes Ferreira, Susana Rainho

Segue o seguinte protocolo de construção.

  1. Toolbar ImageConstrói uma circunferência com 3 cm de raio e centro no centro A.
  2. Toolbar ImageMarca sobre essa circunferência dois pontos B e C.
  3. Toolbar ImageConstrói o segmento [AB].
  4. Toolbar ImageTraça o segmento [BC].
  5. Toolbar ImageAssinala o ponto B' que é a imagem do ponto B pela rotação de centro em O e amplitude 180º
  6. Toolbar ImageTraça o segmento [BB'].

Questão 1

Que nome dás ao segmento [AB]?

Assinale a sua resposta aqui
  • A
  • B
  • C
Verifique minha resposta (3)

Questão 2

Que nome dás ao segmento [BC]?

Assinale a sua resposta aqui
  • A
  • B
  • C
Verifique minha resposta (3)

Questão 3

Que nome dás ao segmento [BB']?

Assinale a sua resposta aqui
  • A
  • B
  • C
Verifique minha resposta (3)

Questão 4

Determina o comprimento da circunferência. Apresenta o resultado em cm, arredondado às décimas. Nota: .

Verifique sua resposta

Questão 5

Determina a área do círculo limitado pela circunferência dada. Apresenta o valor aproximado, em centímetros quadrados, arredondado às centésimas. Nota:

Ângulo ao Centro e Arco da circunferência
Dada uma circunferência, chama-se ângulo ao centro a qualquer ângulo cujo vértice coincide com a circunferência.
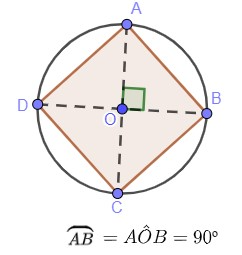
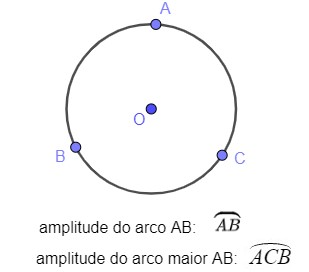
Image
À porção de circunferência compreendida entre dois dos seus pontos chama-se arco da circunferência. A cada ângulo ao centro corresponde um arco da circunferência e a cada arco de circunferência corresponde um ângulo ao centro.
Image
Chama-se amplitude do arco de circunferência à amplitude do ângulo ao centro correspondente. A amplitude do arco AB representa-se por
[center][/center]



Exemplo: Na figura, podemos observar um quadrado inscrito na circunferência. Podemos observar que a amplitude do ângulo ao centro AOB mede 90º. pelo que aamplitude do arco AB mede também 90º.
Image
Nota: Dois pontos A e B da circunferência dividem-na em 2 arcos. Quando dizemos "arco AB" referimo-nos ao arco de menor amplitude. Se nos quisermos referir ao arco de maior amplitude, devemos dizer "arco maior AB" ou "arco ACB".
Image

Questão 6.

Na figura, os vértices da estrela dividem a circunferência de centro O em 5 arcos geometricamente iguais. Determina a amplitude:
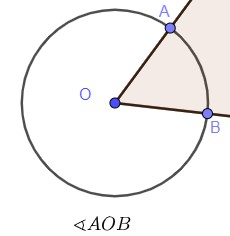
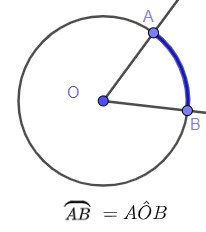
Image

6.1. Do arco AB;

6.1. Do arco AB;

6.2. Do ângulo ao centro COE;

6.3. Do arco CE;

6.4. Do arco maior BD.

Ângulo inscrito na circunferência Chama-se ângulo inscrito a quaquer ângulo cujo vértice seja um ponto da circunferência e cujos lados contenham cordas da circunferência.
Segue o seguinte protocolo de construção. 1. Toolbar ImageConstrói uma circunferência de raio 3 cm. 2. Toolbar ImageDesenha os pontos B, C e D sobre a circunferência. 3. Toolbar ImageConstrói as semirretas BC e BD. 4. Toolbar ImageMede a amplitude do ângulo inscrito CBD. 5. Toolbar ImageMovimenta o ponto B. O que observas? Agora, responde às questões 7 e 8. 5. Toolbar ImageToolbar ImageConstrói o ângulo ao centro CAD e mede a sua amplitude. 6. Toolbar ImageMovimenta o ponto D. O que observas? Agora, responde às questões em falta.

Questão 7

Ao movimentar o ponto B, o que observaste? O que podes concluir acerca de ângulos inscritos no mesmo arco de circunferência?

Questão 8.

Que relação existe entre a amplitude do ângulo inscrito e a amplitude do ângulo ao centro correspondente?

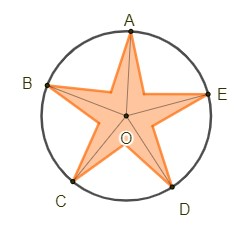
Questão 9.

Observa a figura abaixo. Determina a amplitude dos ângulos, apresentando os cálculos ou justificações necessárias:
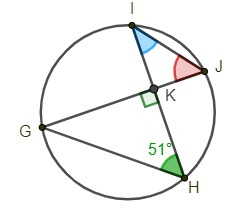
Image

9.1. GJI;

9.2. HIJ.

Questão 10
Observa a figura. Sabe-se que o centro da circunferência é o ponto O, que BC é um diâmetro e que o arco AB mede 50º.
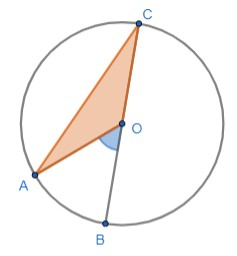
Image

10.1. Classifica o triângulo [AOC] quanto aos lados.

10.2. Determina a amplitude dos ângulos: 10.2.1. AOB

10.2.2. COA

10.2.3 ACB

Questão 11

Na figura, [AB] é um diâmetro da circunferência de centro O.
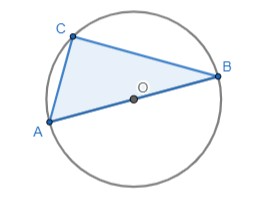
Image

Mostra que [ABC] é um triângulo retângulo.

Novos Materiais

Descobrir recursos

Explorar Tópicos