Le funzioni definite a tratti
Partiamo dal dominio di alcune funzioni...
Qual è la condizione da imporre per il dominio di p(x) (cioè la funzione rappresentata quando lo slider è posto su e=3)?
E per il dominio di q(x) (e=4)?
E per quello di r(x) (e=5)?
E per quello di s(x) (e=6)?
Non ti ho chiesto il dominio delle prime due funzioni perché non c'è scritta la loro equazione, ma come mai?
Magari hai notato che le prime due funzioni sono un po' particolari, sono "a pezzi", non c'è una funzione definita da un'UNICA equazione f(x)=...... come quelle che abbiamo visto finora. Le funzioni così costruite si dicono proprio FUNZIONI DEFINITE A TRATTI e ciascun tratto è limitato solamente a un certo intervallo della x (variabile indipendente). Ti consiglio ora di leggere il paragrafetto a pag.86 del tuo libro.

Una domanda per te: cosa succede secondo te se gli intervalli sui quali sono definiti i tratti si "accavallano"? Ad esempio, se nell'esempio del libro fosse stato il primo tratto per e il secondo per . Si tratta ancora di una funzione? Spiega il perché della tua risposta, pensando a quello che abbiam detto perché si abbia una funzione (se ti è comodo, puoi anche far riferimento dal punto di vista grafico).
Vai a pagina 107 del tuo libro e risolvi qui gli esercizi 58 e 59.
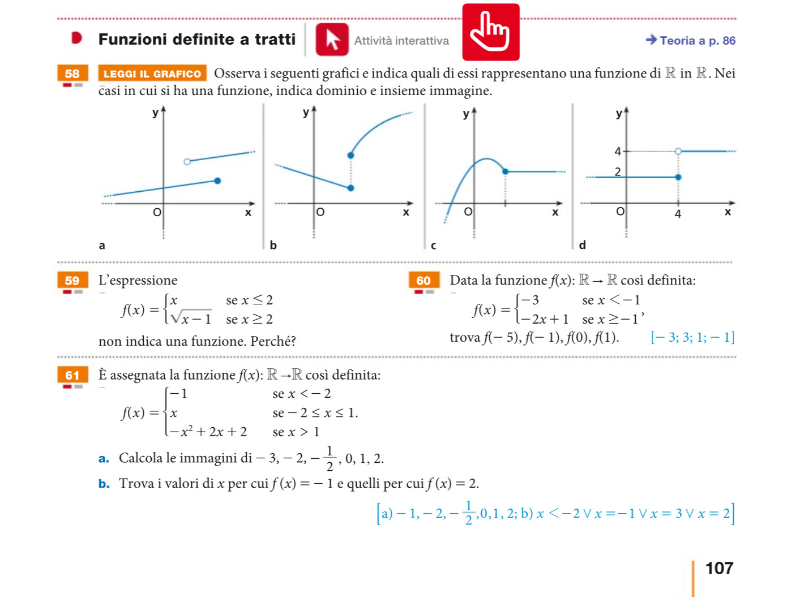
Finora abbiamo visto che i due tratti della funzione sono "uniti" (uno inizia esattamente nello stesso punto in cui finisce l'altro) e ti ho fatto riflettere su cosa succede se gli intervalli della x per i quali sono definiti i tratti si "accavallano", ma i tratti potrebbero anche essere "staccati", come nella costruzione qui sotto.
Modificando la costruzione qui sopra e la definizione dei tratti, risolvi gli esercizi 60 e 61 pag.107 del tuo libro.