Модель паралельних прямих Лобачевського
Припустимо, у нас є пряма а і точка А, що не
належить їй. Спробуйте уявити, що через точку А можна провести не одну, а дві прямі, паралельні а, так, щоб вони не збігалися.
Така побудова не може існувати у звичній для нас
евклідовій геометрії. Проте в геометрії, описаній Миколою Лобачевським, яка
була доведена ще в 1871 році (вже після смерті вченого), через точку А може проходити кілька прямих,
паралельних прямій а.
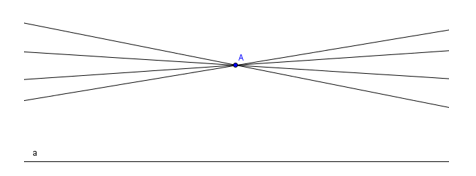
Пучок паралельних прямих Лобачевського приблизно виглядає
так:
Для того щоб проілюструвати і краще зрозуміти цей принцип
паралельності, побудуємо в GeoGebra наближену модель паралельних прямих
Лобачевського. Наближену – тому що, по суті, будувати її ми будемо в евклідовій
геометрії.
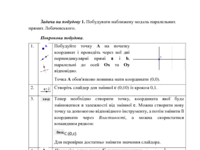
Задача на побудову 1. Побудувати наближену модель паралельних прямих Лобачевського.
Модель готова і працює, але, все ж, не зрозуміло, чому ці відрізки, візуально
перетинаються і при цьому являють собою паралельні прямі. Можна припустити, що тільки при малих відстанях, таких, як від Землі до Сонця, ці прямі будуть «зливатися» у
паралельну. На великих же відстанях вони «викривляються».