Funkční závislosti, volný pád
V denním životě, v přírodě, v technice a hlavně v matematice se neustále setkáváme s funkčními závislostmi jedné veličiny (např. y) na druhé (např. x). Například, zkoumáme - li vývoj epidemie, zaznamenáváme počet nakažených každý den, nebo denní počet hospitalizovaných, nebo týdenní přírustky počtu nakažených. Nezávislou proměnnou je zde čas, funkční hodnoty jsou počty pacientů. Ačkoliv je čas spojitou veličinou (z reálného intervalu), je jeho diskretizace dána frekvencí měření. Počet pacientů je diskréní náhodná veličina (spočetná), přesto ji můžeme pro matematické modelování a odhady trendu považovat za veličinu spojitou.
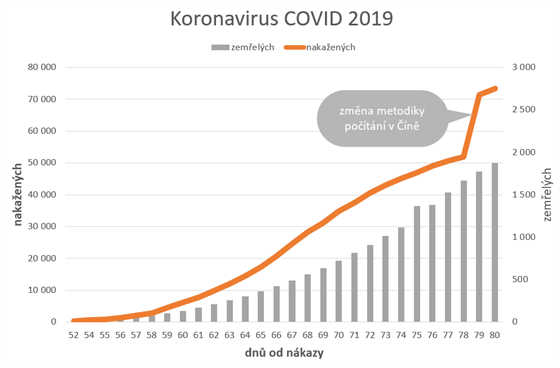 Přísné dělení veličin na spojité a diskrétní je matematický formalismus, jenž dává definicím zdání dokonalosti, v praktických aplikací jsou ale data vždy diskrétní. To nám ale nebrání modelovat je jako veličiny spojité a používat pro jejich analýzu všechny výsledky infninitesimálního počtu.
V našem kurzu předpokládáme, že znáte základní vlastnosti funkce (prostá, rostoucí, klesající, sudá, lichá, periodická), umíte určit definiční obor i že nakreslíte zpaměti graf elementárních funkcí (mocninná, racionální, exponenciální, logaritmická, goniometrická).
Procvičte se ze znalostí grafu základních funkcí v prostředí Memrise. Je třeba se jen přihlásit účtem Google nebo Facebook.
Ať již zkoumáme jakoukoliv závislost, všechny mají jednu společnou vlastnost: ke každé hodnotě nezávislé proměnné existuje nejvýše jedna reálná hodnota zkoumané závislé veličiny.
Zkoumáme-li např. volný pád , můžeme zaznamenávat výšku tělesa h(t) v daném čase t, nebo můžeme zkoumat velikost okamžité rychlosti pádu v(t) v okamžiku t. Nemůžeme v daném čase t zaznamenat dvě různé rychlosti, dvě různé výšky.
Volný pád v homogenním tíhovém poli (odpor prostředí zanedbáváme) je rovnoměrně zrychlený přímočarý pohyb se zrychlením rovným tíhovému zrychlení g. Proto je grafem h(t) parabola, kdežto závislost v(t) = g.t je lineární.
Přísné dělení veličin na spojité a diskrétní je matematický formalismus, jenž dává definicím zdání dokonalosti, v praktických aplikací jsou ale data vždy diskrétní. To nám ale nebrání modelovat je jako veličiny spojité a používat pro jejich analýzu všechny výsledky infninitesimálního počtu.
V našem kurzu předpokládáme, že znáte základní vlastnosti funkce (prostá, rostoucí, klesající, sudá, lichá, periodická), umíte určit definiční obor i že nakreslíte zpaměti graf elementárních funkcí (mocninná, racionální, exponenciální, logaritmická, goniometrická).
Procvičte se ze znalostí grafu základních funkcí v prostředí Memrise. Je třeba se jen přihlásit účtem Google nebo Facebook.
Ať již zkoumáme jakoukoliv závislost, všechny mají jednu společnou vlastnost: ke každé hodnotě nezávislé proměnné existuje nejvýše jedna reálná hodnota zkoumané závislé veličiny.
Zkoumáme-li např. volný pád , můžeme zaznamenávat výšku tělesa h(t) v daném čase t, nebo můžeme zkoumat velikost okamžité rychlosti pádu v(t) v okamžiku t. Nemůžeme v daném čase t zaznamenat dvě různé rychlosti, dvě různé výšky.
Volný pád v homogenním tíhovém poli (odpor prostředí zanedbáváme) je rovnoměrně zrychlený přímočarý pohyb se zrychlením rovným tíhovému zrychlení g. Proto je grafem h(t) parabola, kdežto závislost v(t) = g.t je lineární.
 Přísné dělení veličin na spojité a diskrétní je matematický formalismus, jenž dává definicím zdání dokonalosti, v praktických aplikací jsou ale data vždy diskrétní. To nám ale nebrání modelovat je jako veličiny spojité a používat pro jejich analýzu všechny výsledky infninitesimálního počtu.
V našem kurzu předpokládáme, že znáte základní vlastnosti funkce (prostá, rostoucí, klesající, sudá, lichá, periodická), umíte určit definiční obor i že nakreslíte zpaměti graf elementárních funkcí (mocninná, racionální, exponenciální, logaritmická, goniometrická).
Procvičte se ze znalostí grafu základních funkcí v prostředí Memrise. Je třeba se jen přihlásit účtem Google nebo Facebook.
Ať již zkoumáme jakoukoliv závislost, všechny mají jednu společnou vlastnost: ke každé hodnotě nezávislé proměnné existuje nejvýše jedna reálná hodnota zkoumané závislé veličiny.
Zkoumáme-li např. volný pád , můžeme zaznamenávat výšku tělesa h(t) v daném čase t, nebo můžeme zkoumat velikost okamžité rychlosti pádu v(t) v okamžiku t. Nemůžeme v daném čase t zaznamenat dvě různé rychlosti, dvě různé výšky.
Volný pád v homogenním tíhovém poli (odpor prostředí zanedbáváme) je rovnoměrně zrychlený přímočarý pohyb se zrychlením rovným tíhovému zrychlení g. Proto je grafem h(t) parabola, kdežto závislost v(t) = g.t je lineární.
Přísné dělení veličin na spojité a diskrétní je matematický formalismus, jenž dává definicím zdání dokonalosti, v praktických aplikací jsou ale data vždy diskrétní. To nám ale nebrání modelovat je jako veličiny spojité a používat pro jejich analýzu všechny výsledky infninitesimálního počtu.
V našem kurzu předpokládáme, že znáte základní vlastnosti funkce (prostá, rostoucí, klesající, sudá, lichá, periodická), umíte určit definiční obor i že nakreslíte zpaměti graf elementárních funkcí (mocninná, racionální, exponenciální, logaritmická, goniometrická).
Procvičte se ze znalostí grafu základních funkcí v prostředí Memrise. Je třeba se jen přihlásit účtem Google nebo Facebook.
Ať již zkoumáme jakoukoliv závislost, všechny mají jednu společnou vlastnost: ke každé hodnotě nezávislé proměnné existuje nejvýše jedna reálná hodnota zkoumané závislé veličiny.
Zkoumáme-li např. volný pád , můžeme zaznamenávat výšku tělesa h(t) v daném čase t, nebo můžeme zkoumat velikost okamžité rychlosti pádu v(t) v okamžiku t. Nemůžeme v daném čase t zaznamenat dvě různé rychlosti, dvě různé výšky.
Volný pád v homogenním tíhovém poli (odpor prostředí zanedbáváme) je rovnoměrně zrychlený přímočarý pohyb se zrychlením rovným tíhovému zrychlení g. Proto je grafem h(t) parabola, kdežto závislost v(t) = g.t je lineární.Hmotnost tělesa nemá na pohyb vliv (Aristoteles x Galileo, Youtube).
Grafy elementárních funkcí
Napište do příkazového řádku předpis funkcí f1(x) = |x|, f2(x) = sin x, f3(x) = tan x, f4(x) = cosh x
Seznam užitečných konstant a funkcí GeoGebry - https://wiki.geogebra.org/en/Predefined_Functions_and_Operators
Nástroj posuvník  je užitečný pro zkoumání vlivu parametru na graf funkce. Funkce p(x) = ax je vykreslena fialově pro nastavenou hodnotu posuvníku a.
je užitečný pro zkoumání vlivu parametru na graf funkce. Funkce p(x) = ax je vykreslena fialově pro nastavenou hodnotu posuvníku a.
 je užitečný pro zkoumání vlivu parametru na graf funkce. Funkce p(x) = ax je vykreslena fialově pro nastavenou hodnotu posuvníku a.
je užitečný pro zkoumání vlivu parametru na graf funkce. Funkce p(x) = ax je vykreslena fialově pro nastavenou hodnotu posuvníku a.Literatura
Prezentace k přednášce "Funkce", Google Slides
Prezentace k přednášce "Infinitesimální počet", Google Slides