Addition von Brüchen
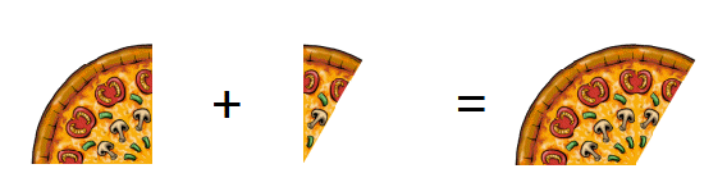
Kurzinformation
- Thema: Addition von Brüchen
- 6. Schulstufe, Mathematik
- Dauer: 3 Unterrichtseinheiten
- Gesamtmaterial
- Spezielle Materialien: feste DIN-A5-Blätter (doppelt so viele wie SchülerInnen in der Klasse sind); grüne und rote Stifte; evtl. Scheren, wenn nur DIN-A4-Blätter vorhanden sind; verschiedenfarbige Kreiden und Stifte; Freiarbeitsplan (ausgedruckt); Arbeitblätter 1, 2 und 3 (ausgedruckt); Spielanleitung "Triff die 2" (ausgedruckt) und Spielmaterialien (ausgedruckt, ausgeschnitten und evtl. laminiert); Computer, Laptops, Tablets oder evtl. Smartphones
Vorwissen und Voraussetzungen
Die SchülerInnen wissen,...
- ...welche Bedeutung Zähler, Nenner und Bruchstrich haben.
- ...welche verschiedenen Brucharten es gibt.
- ...wie unechte Brüche in gemischte Zahlen umgewandelt werden und umgekehrt.
- ...wie Brüche erweitert und gekürzt werden.
- ...wie Brüche graphisch dargestellt werden und umgekehrt.
- ...wie Brüche miteinander verglichen und geordnet werden können.
Lernergebnisse und Kompetenzen
Die SchülerInnen können...
- ...graphische und symbolische Darstellungen von Brüchen miteinander verknüpfen.
- ...gleichnamige Brüche addieren.
- ...ungleichnamige Brüche addieren.
- ...gemischte Zahlen addieren.
Unterrichtsablauf
Bevor die Addition von Brüchen sowohl auf symbolischer als auch auf ikonischer Ebene eingeführt wird, werden diese beiden Darstellungen von Brüchen mithilfe eines Dominos wiederholt. Mit diesem Wissen als Basis kann dann auf die Addition von Brüchen übergegangen werden, wobei zunächst gleichnamige Brüche, anschließend ungleichnamige Brüche und zuletzt gemischte Zahlen miteinander addiert werden. Dies soll in der letzten Einheit geübt und vertieft werden, indem die SchülerInnen bei einer Freiarbeit verschiedenste Aufgaben bearbeiten sollen.
Aktivität 1 (40 min): Domino zur Wiederholung der verschiedenen Bruchdarstellungen
Materialien: feste DIN-A5-Blätter (doppelt so viele wie SchülerInnen in der Klasse sind); grüne und rote Stifte; evtl. Scheren, wenn nur DIN-A4-Blätter vorhanden sind
Dieses Dominospiel eignet sich hervorragend, um den Wechsel zwischen symbolischer und graphischer Darstellung von Brüchen enaktiv zu üben und zu wiederholen.
Das Domino entsteht dadurch, dass jede(r) SchülerIn zwei DIN-A5-Blätter Papier erhält und auf das eine Blatt mit Grün einen Anteil zeichnet (beispielsweise als Kreis oder Rechteck) und auf das andere in Rot den dazugehörigen Bruch als Symbol anschreibt. Dabei sind - neben gemischten Zahlen - sowohl erweiterte, als auch gekürzte Brüche erlaubt. Dies soll verhindern, dass später beim Spielen des Dominos oft dieselben Brüche vorkommen. Die jeweiligen Sitznachbarn kontrollieren die Aufgabe. Anschließend werden die grünen und die roten Kartensätze eingesammelt, getrennt gemischt und ausgeteilt, sodass jede(r) SchülerIn eine grüne und eine rote Karte erhält. Um Ein-Schüler-Kreise zu verhindern, kontrollieren alle SchülerInnen, ob sie nicht schon zwei passende Karten erhalten haben. In diesem Fall müssten die Karten nochmals getauscht werden. Dann werden die SchülerInnen selbst zu Dominosteinen, indem die grüne Karte in die linke Hand kommt und die rote in die rechte. Die Aufgabe lautet nun folgendermaßen: Jede linke Hand soll eine passende rechte Hand finden, sodass die Karten zueinanderpassen. Dadurch sollte eine Verkettung der SchülerInnen entstehen. Bei der Suche nach der bzw. dem richtigen PartnerIn darf nicht gesprochen werden. Die SchülerInnen sollten selbst die Erkenntnis erlangen, dass dadurch Kreise entstehen und wahrscheinlich auch mehrere. Je größer die Kreise sind, desto herausfordernder wird das Dominospiel.
Wenn das Domino mit diesen selbstgebastelten Karten öfter gespielt werden soll, können die Karten noch zusätzlich laminiert werden, damit sie robuster sind.

Aktivität 2 (60 min): Einführung der Addition von Brüchen
Materialien: verschiedenfarbige Kreiden und Stifte
Bei der Einführung der Addition von Brüchen ist vor allem die beim Domino nochmals wiederholte graphische Darstellungsform sehr hilfreich. Denn mit Hilfe dieser kann sowohl die Addition von gleichnamigen Brüchen als auch die Addition von ungleichnamigen Brüchen gut veranschaulicht werden.
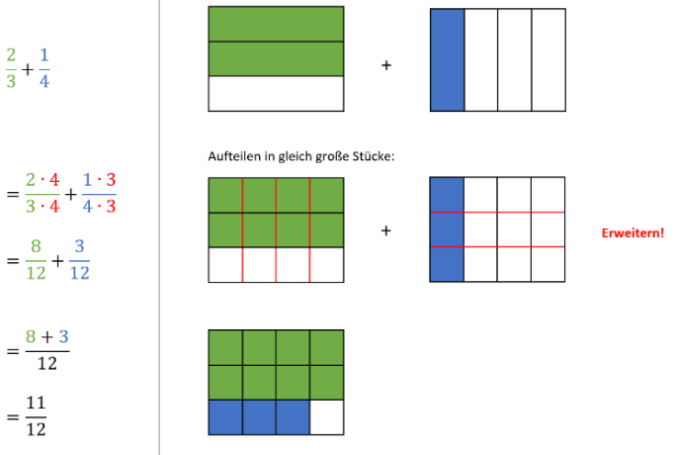
Die Addition gleichnamiger Brüche und die Addition ungleichnamiger Brüche werden auf die gleiche Art und Weise eingeführt: Die Tafel wird dabei in der Mitte geteilt. Auf der linken Seite wird die analytische Denkweise und rechts die geometrische Interpretation angeführt. Wie dieser Tafelaufschrieb für die Addition von gleichnamigen und ungleichnamigen Brüchen aussehen kann, zeigen folgende zwei Bilder. So sollen die SchülerInnen die symbolische Darstellung der Addition von Brüchen durch die ikonische Darstellung besser verstehen. Anschließend wird dies anhand einiger Beispiele geübt. Dabei wird jedoch so vorgegangen, dass zuerst die Addition von gleichnamigen Brüchen eingeführt wird und danach ein paar Beispiele (zuerst gemeinsam, anschließend jeder für sich) gerechnet werden. Dann erst wird die Addition von ungleichnamigen Brüchen - wiederum mit dem zweiteiligen Tafelaufschrieb - eingeführt und mit Beispielen geübt. Anschließend wird noch die Addition von gemischten Zahlen eingeführt und durch Beispiele geübt. Durch das Üben an den Beispielen sollen die SchülerInnen schlussendlich auch erkennen, dass das Rechnen viel schneller und leichter ist, als Kästchen zu zeichnen.
Neben dem zweiteiligen Tafelaufschrieb und den Beispielen zur Übung sollen die SchülerInnen auch ein Rezept für die Addition von Brüchen in ihrem Heft festhalten. Dazu sollen sie Folgendes aufschreiben:
Rezept zur Addition von Brüchen:
- Überprüfe, ob die Brüche den gleichen Nenner haben! Ist das nicht der Fall, dann bestimme einen gemeinsamen Nenner und erweitere die Brüche so, dass sie den gleichen Nenner haben!
- Addiere die Zähler der Brüche, der Nenner bleibt gleich!
- Wenn möglich, dann kürze das Ergebnis und schreibe als gemischte Zahl an!
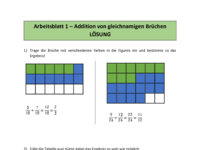
Tafelbild - Addition von gleichnamigen Brüchen
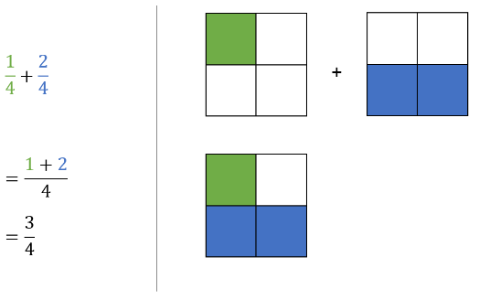
Tafelbild - Addition von ungleichnamigen Brüchen
Beispiele zur Übung
Lösungen der Beispiele zur Übung
Aktivität 3 (50 min): Freiarbeit zur Übung der Addition von Brüchen
Materialien: Freiarbeitsplan (ausgedruckt); Arbeitblätter 1, 2 und 3 (ausgedruckt); Spielanleitung "Triff die 2" (ausgedruckt) und Spielmaterialien (ausgedruckt, ausgeschnitten und evtl. laminiert); Computer, Laptops, Tablets oder evtl. Smartphones
Die SchülerInnen erhalten den Freiarbeitsplan in ausgedruckter Form. Dieser enthält verpflichtende Aufgaben und Wahl- sowie Bonusaufgaben, welche auch als solche gekennzeichnet sind. Alle Aufgaben (bis auf die Bonusaufgabe) sind in Einzelarbeit zu bearbeiten, wobei die SchülerInnen die Reihenfolge sowie die für die einzelnen Aufgaben notwendige Zeit selbst bestimmen dürfen. Ist eine Aufgabe erledigt, so sollen dies die SchülerInnen in der entsprechenden Spalte (Bleistift-Symbol) durch ein Häckchen kennzeichnen. Außerdem sollen sie auch angeben, wie es ihnen bei dieser Aufgabe ergangen ist. Dazu sollen sie in der entsprechenden Spalte (drei Smileys) den für sie passenden Smiley einzeichnen.
Der Freiarbeitsplan sowie alle Aufgaben der Freiarbeit sind in einem GeoGebra-Book gesammelt.
Vorlage des Freiarbeitsplans zur Addition von Brüchen
Hausübung
Falls die SchülerInnen die Pflichtaufgaben oder die entsprechend verpflichtende Anzahl der Wahlaufgaben während des Unterrichts nicht fertiggestellt haben, so ist der Rest als Hausübung zu erledigen.
Überprüfen des Lernerfolges
Die Lehrperson kann während der Unterrichtseinheit den Lernerfolg der SchülerInnen durch Kontrollieren der Aufgaben des Freiarbeitsplans überprüfen. Beim Freiarbeitsplan ist dafür eine extra Spalte (Häkchen-Symbol) vorgesehen. In dieser kann die Lehrkraft bestenfalls mittels eines Stempels oder ansonsten durch ein Häkchen festhalten, welche Aufgaben schon kontrolliert wurden. Der Vorteil eines Stempels gegenüber eines einfachen Häkchens wäre dabei, dass dieser nicht von den SchülerInnen gefälscht werden kann.
Falls die SchülerInnen in der Stunde nicht mit der Freiarbeit fertig werden, kann diese als Hausübung aufgegeben werden. Die Kontrolle erfolgt auch dann durch die Lehrkraft, indem die SchülerInnen die bearbeiteten Aufgaben der Lehrperson am Anfang der nächsten Stunde abgeben.
Lösungen der Pflichtaufgaben
Links zu Materialien und Quellen
Materialien:
Gesamtmaterial
Quellen:
- Barzel, B., Büchter, A. & Leuders, T. (2019). Mathematik Methodik. Handbuch für die Sekundarstufe I und II (10. Aufl.). Berlin: Cornelsen.
- Baumann, C., Beck, F., Mengdehl, M., Zähringer, K. & Leuders, T. (2008). "Triff die Zwei". Ein Spiel zur Übung von Bruchaddition. PM Praxis der Mathematik in der Schule, 22, 30-33.
- Glade, M. (2013). "Rechnen ist viel leichter und schneller als Kästchen zu zeichnen". Die Rechenregel zum Anteil vom Anteil durch Fortschreitende Schematisierung erarbeiten. PM Praxis der Mathematik in der Schule, 52, 20-25.
- Hasemann, K. (1986). Bruchvorstellungen und die Addition von Bruchzahlen. mathematik lehren, 16, 16-19.
- Kramer, M. (2014). Mathematik als Abenteuer. Band 2: Algebra und Vektorrechnung (3. Aufl.). Hallbergmoos: Aulis.
- Marxer, M. & Wittmann, G. (2011). Förderung des Zahlenblicks - Mit Brüchen rechnen, um ihre Eigenschaften zu verstehen. MU Der Mathematikunterricht, 57, 25-34.