Mapping Triangles
The core elements of performance required by this task are:
Geometry 8.G
Understand congruence and similarity using physical models, transparencies, or geometry software.
2. Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them.
3. Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates.
4. Understand that a two-dimensional figure is similar to another if the second can be obtained from the first by a sequence of rotations, reflections, translations, and dilations; given two similar two-dimensional figures, describe a sequence that exhibits the similarity between them.
Vanessa drew five triangles on a coordinate plane. She labeled each triangle with letters A through E. The vertices of Triangle A are (4,1), (6,6), and (7,1).
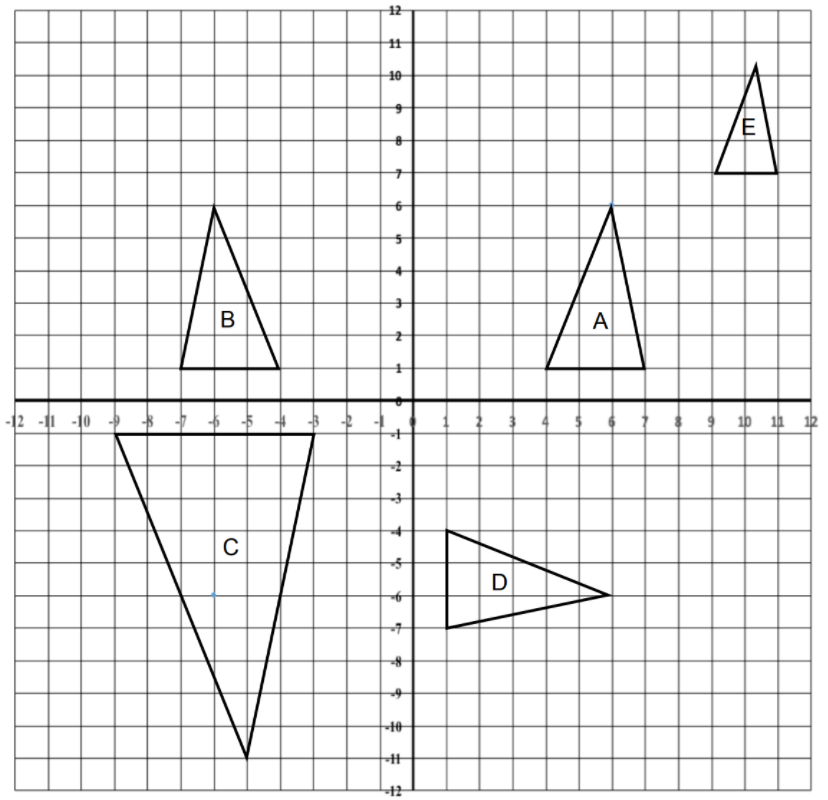
What is the area of Triangle A? Explain how you figured it out.
Triangle A is congruent to Triangle B.
Describe a transformation that maps Triangle A to Triangle B.
List the corresponding vertices between the two triangles.
Triangle A is similar to Triangle C.
Describe the set of transformations that could verify that they are similar.
Triangle A can be rotated about the origin to show that it is congruent to Triangle D.
What is the direction and angle of the rotation? How do you know for sure?
Triangle A maps Triangle E through a dilation.
What is the scale factor of the dilation? Explain how you figured it out.