Die Sinusfunktion
Von der Winkelbeziehung zur Funktionsgleichung
Die meisten von uns sollten schon in der Mittelstufe als eine Winkelbeziehung im rechtwinkligen Dreieck kennengelernt haben, als "Sinus Alpha ist gleich Gegenkathete durch Hypothenuse":
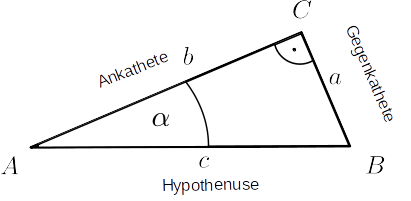Eine Funktionsgleichung erhält man, wenn man einen Zeiger in einem Einheitskreis rotieren lässt (siehe hier).
Eine Funktionsgleichung erhält man, wenn man einen Zeiger in einem Einheitskreis rotieren lässt (siehe hier). Ein Steckbrief für die Sinusfunktion
Die Sinusfunktion hat einige Merkmale, an denen man sie gut erkennen kann:
- Die Sinusfunktion ist periodisch. Der blau markierte Teil des oben abgebildeten Funktionsgraphen wiederholt sich unendlich oft in beide Richtungen, also für und für . Das Intervall, in dem die erste (blaue) Periode der Sinusfunktion liegt, ist . Man sagt auch, die Sinusfunktion hat eine Periodenlänge von .
- Die Nullstellen der Sinusfunktion liegen bei einem Vielfachen der Kreiszahl . Also , wobei z eine beliebige ganze Zahl ist: . Bei den Nullstellen liegen auch die Wendepunkte der Funktion: .
- Der Hochpunkt der ersten Periode liegt bei . Weil die Sinusfunktion periodisch ist, gibt es jeweils mit einem Abstand von nach links und nach rechts auf der Abszisse verschoben unendlich viele weitere Hochpunkte mit . Diese haben alle den Funktionswert .
- Der Tiefpunkt der ersten Periode liegt bei . Weil die Sinusfunktion periodisch ist, gibt es jeweils mit einem Abstand von nach links und nach rechts auf der Abszisse verschoben unendlich viele weitere Tiefpunkte mit . Diese haben alle den Funktionswert .