Injective , Surjective or Bijective
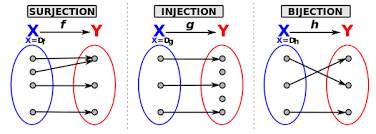
A function f : Z → Z is defined as f (n) = 2n +1.
Verify whether this function is injective and whether it is surjective.
This function is injective. To see this, suppose m, n ∈ Z and f (m) = f (n).
This means 2m+1 = 2n+1, from which we get 2m = 2n, and then m = n.
Thus, f is injective. This function is not surjective.
To see this notice that f (n) is odd for all n ∈ Z.
So, given the (even) number 2 in the codomain Z, there is no n with f (n) = 2.
Explanation
a) Function Definition: The function f: Z→Z is defined as f(n) = 2n + 1, where n is an integer.
b) Injective (One-to-One) Property:
A function is injective if each element in the domain maps to a unique element in the codomain. To verify if f is injective, we need to show that whenever f(m) = f(n) for m, n Z, then m = n.
Let m, n
Z, then m = n.
Let m, n Z such that f(m) = f(n). This means 2m + 1 = 2n + 1.
-By subtracting 1 from both sides of the equation, we get 2m = 2n.
-Further dividing both sides by 2, we obtain m = n.
Since m and n are equal, the function f is injective.
c) Surjective (Onto) Property: A function is surjective if every element in the codomain has at least one
pre-image in the domain. To check if f is surjective, we need to ensure that for every integer m in the codomain Z, there exists an integer n in the domain Z such that f(n) = m.
Notice that f(n) is odd for all integers n because it is in the form 2n + 1, where 2n is even, and adding 1
makes it odd. Now, consider the (even) number 2 in the codomain Z. There is no integer n that satisfies
f(n) =2, because f(n)is always odd and cannot be equal to an even number.
Since there is no integer n that maps to the (even) number 2 in the codomain, the function f is not surjective.
In summary, the function f: Z→Z defined as f(n) = 2n + 1 is injective but not surjective. It is injective because distinct integers in the domain have distinct images in the codomain. However, it is not surjective
because not every element in the codomain has a pre-image in the domain. Specifically, there is no integer n such that f(n) = 2.
Z such that f(m) = f(n). This means 2m + 1 = 2n + 1.
-By subtracting 1 from both sides of the equation, we get 2m = 2n.
-Further dividing both sides by 2, we obtain m = n.
Since m and n are equal, the function f is injective.
c) Surjective (Onto) Property: A function is surjective if every element in the codomain has at least one
pre-image in the domain. To check if f is surjective, we need to ensure that for every integer m in the codomain Z, there exists an integer n in the domain Z such that f(n) = m.
Notice that f(n) is odd for all integers n because it is in the form 2n + 1, where 2n is even, and adding 1
makes it odd. Now, consider the (even) number 2 in the codomain Z. There is no integer n that satisfies
f(n) =2, because f(n)is always odd and cannot be equal to an even number.
Since there is no integer n that maps to the (even) number 2 in the codomain, the function f is not surjective.
In summary, the function f: Z→Z defined as f(n) = 2n + 1 is injective but not surjective. It is injective because distinct integers in the domain have distinct images in the codomain. However, it is not surjective
because not every element in the codomain has a pre-image in the domain. Specifically, there is no integer n such that f(n) = 2.
Consider the cosine function cos : R→ R. Decide whether this function is injective and whether it is surjective. What if it had been defined as cos : R → [−1,1]?