Pendientes, pozos, sandías notables... y la recta de Euler
ACTIVIDAD 1. Los pendientes.
Suponiendo que el material con el que están hechos los pendientes tienen la misma densidad, ¿cuál es el centro de gravedad de los pendientes de la figura?
ACTIVIDAD 2. ¿En qué posición tenemos que colocar el pozo para que esté a la misma distancia de las tres casas?
Dibújalo en la siguiente ventana:
ACTIVIDAD 3. Tenemos una sandía con forma de triángulo y queremos cortar un trozo circular. ¿Cómo podríamos hacerlo para obtener el mayor círculo posible?
Dibújalo en la siguiente ventana:
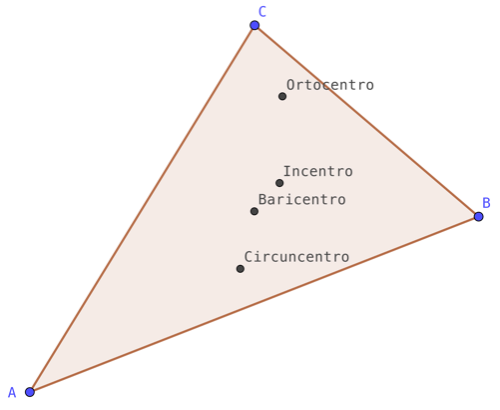
ACTIVIDAD 4. Los puntos notables de un triángulo.
Construye los cuatro puntos notables (baricentro, circuncentro, incentro y ortocentro) del triángulo ABC que aparece en la siguiente ventana, siguiendo los pasos indicados más abajo.
Escondiendo los punto, rectas,… auxiliares que vas utilizando para construirlos, debes de llegar a una construcción similar a la que aparece en la siguiente figura:
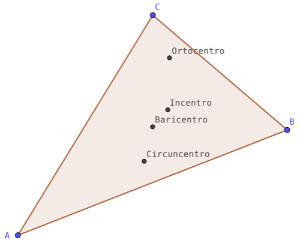
Pasos a seguir:
- Construye un triángulo cualquiera ABC.
- Construye el baricentro del triángulo ABC (recuerda que el baricentro es la intersección de las tres medianas del triángulo). Utiliza la herramienta "medio o centro"
 .
. - Renombra el punto como "baricentro" y haz que la etiqueta sea visible.
- Esconde las tres medianas, que solo quede visible el baricentro.
- Construye el incentro del triángulo ABC (recuerda que el incentro es las intersección de las tres bisectrices del triángulo). Utiliza la herramienta "bisectriz"
 .
. - Renombra el punto como "incentro" y haz que la etiqueta sea visible.
- Comprueba que efectivamente es el incentro dibujando la circunferencia inscrita del triángulo.
- Esconde las tres bisectrices.
- Construye el circuncentro del triángulo ABC (recuerda que el circuncentro es la intersección de las tres mediatrices del triángulo). Utiliza la herramienta "mediatriz"
 .
. - Renombra el punto como "circuncentro" y haz que la etiqueta sea visible.
- Comprueba que efectivamente es el circuncentro dibujando la circunferencia circunscrita del triángulo.
- Esconde las tres mediatrices.
- Construye el ortocentro del triángulo ABC (recuerda que el ortocentro es la intersección de las tres alturas del triángulo). Utiliza la herramienta "perpendicular"
 .
. - Renombra el punto como "ortocentro" y haz que la etiqueta sea visible.
- Esconde las tres alturas.
- En este momento deberías de tener visible solamente el triángulo y los cuatro puntos notables del triángulo ABC: el baricentro, el incentro, el circuncentro y el ortocentro. Haz que el triángulo cambie de forma (pinchando en uno de los vértices y arrastrándolo) y observa cómo se mueven los cuatro puntos. ¡Explora!
Después de realizar el paso 16 anterior, contesta a las siguientes preguntas:
Pregunta 1
¿Existe un tipo de triángulo en donde los cuatro puntos coinciden? Explica por qué.
Pregunta 2
¿Existe un tipo de triángulo en donde los cuatro puntos están alineados? Explica por qué.
¡¡Última pregunta!! Existe una relación entre 3 de los 4 puntos notables de un triángulo (baricentro, circuncentro, incentro y ortocentro). ¿Sabrías decir cuál es? Explícala más abajo y dibuja esta relación en la ventana de arriba. Pista: Euler sabía mucho de triángulos...