aperiodic patterns
aperiodic
In aperiodic tilings one cannot find to translations that picture the tiling on itself. De girih tiles have got the potential to generate such tilings: 10-fold symmetry and a division rule. It’s clear that a lot of decorations are regular although they make use of pentagons or decagons. In previous activities of this book you can find a lot of examples of regular patterns. But Lu and Steinhardt are pointing to some unique examples to illustrate that this potential of the girih tiles effectively found use.
division rule
The tiles in Maragha (1200 AC) are decorated with a second pattern that doesn’t match with the symmetries and angles of the line pattern of the giri tiles.
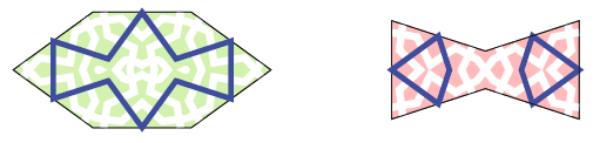
This is no longer the case in a spandrel of the Darb-e Imam shrine in Isfahan traditionally dated in 1453 AC. In it two decorative layers can be distinguished, based on the same girih tiles. We learned from Penrose that in an infinite Penrose tiling the ratio between kites and darts equals the golden number benadert. This irrational ratio is a proof of aperiodicity.
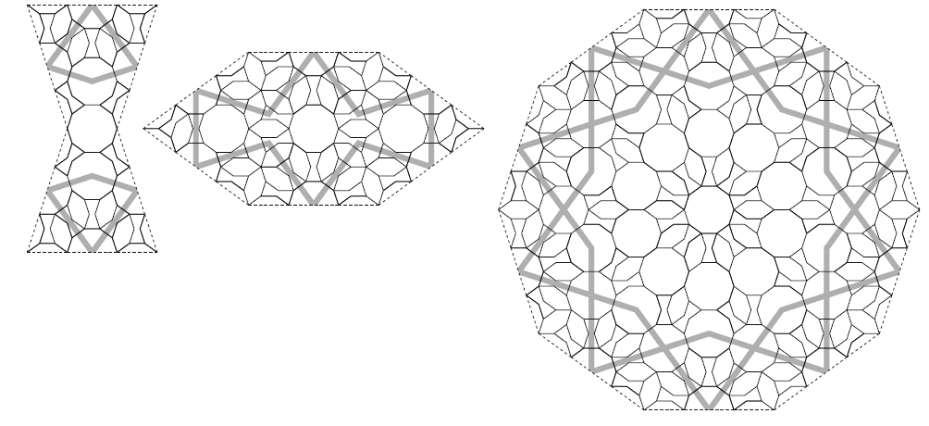
For girih tiles too we can make such calculations. First we define the division rules for decagon, bow tie and hexagon. The properties of this transformation can be written in a matrix. If this matrix has got irrational eigenvalues, it proves aperiodicity. Lu en Steinhardt found the same ratio in the ratio between hexagons and bow ties, proving aperiodicity. Below is a picture of a division of bow tie, hexagon and decagon, drawn by Cromwell.