Betonin puristuslujuus

Rakennustekniikan alalla betonin lujuus on kriittinen asia. Betonin oletetaan kestävän tiettyjä rasituksia, ja jos betonin lujuus ei täyttäisikään vaadittuja normeja, rakenteiden ja rakennuksien kestävyydestä ei voitaisi olla varmoja. Tämän vuoksi valmistettavan betonin lujuutta mitataan, ja tähän on olemassa omat metodinsa. Materiaalin vahvuutta mitataan useilla mittareilla, mutta puhutaan nyt rakentamisen kannalta tärkeimmästä, eli puristuslujuudesta.
Puristuslujuus; mitä se on? Ajattele pino tiiliä toinen toistensa päällä. Ei anneta sen ajatuksen häiriätä, että moinen pino toki kaatuisi: kun tiilistä rakennetaan talo, rakennelma toki tukee itsensä tukevaksi. Puristuslujuus tarkoittaa sitä, kuinka paljon tiili kestää kasaan puristavaa voimaa. Tässä äsken esitelty ajatusleikki tulee hyvin konkreettiseksi: alimpien tiilien pitää kestää koko yläpuolellaan olevan seinän paino. Voidaan sanoa, että alimman tiilen pitää kestää talon seinän korkuinen pino muita tiiliä itsensä päällä. Tätä tarkoittaa puristuslujuus. Sitä mitataan konkreettisesti Newtoneina (voiman yksikkö) per neliömetri (pinta-alayksikkö).
Betonia on valmistettu nyt vuo vuosikymmeniä. Aina, kun valmistetaan uutta betonia, siitä valmistetaan samalla testikappaleita, kuution muotoisia palikoita. Näiden palikoiden puristuslujuutta voidaan nyt mitata hyvin suoraviivaisella testillä: palikkaa puristetaan prässissä puristusvoimaa pikkuhiljaa nostaen, kunnes palikka hajoaa. Tieto siitä, millä puristuksella palikka viimein hajosi, otetaan ylös.
Vuosikymmenien aikana on siis saatu asiasta niin sanottu tietokanta: suuri aineisto tarkkaa mittaustietoa asiasta. Nyt, kun rakentajat valmistavat uutta sementtiä, he mittaavat sen puristuslujuuden, ja vertaavat, onko saadun betonin lujuus sitä, mitä sen ”pitäisi” olla; siis mitä tietokannassa näyttää olevan vallitseva tieto. Kysymys kuuluukin, miten juuri saatua mittausta pitäisi verrata mainittuun suureen tietokantaan? Ratkaisu on sama, mikä se insinöörimatematiikassa usein on: muodostetaan tietokannasta ensin matemaattinen malli.
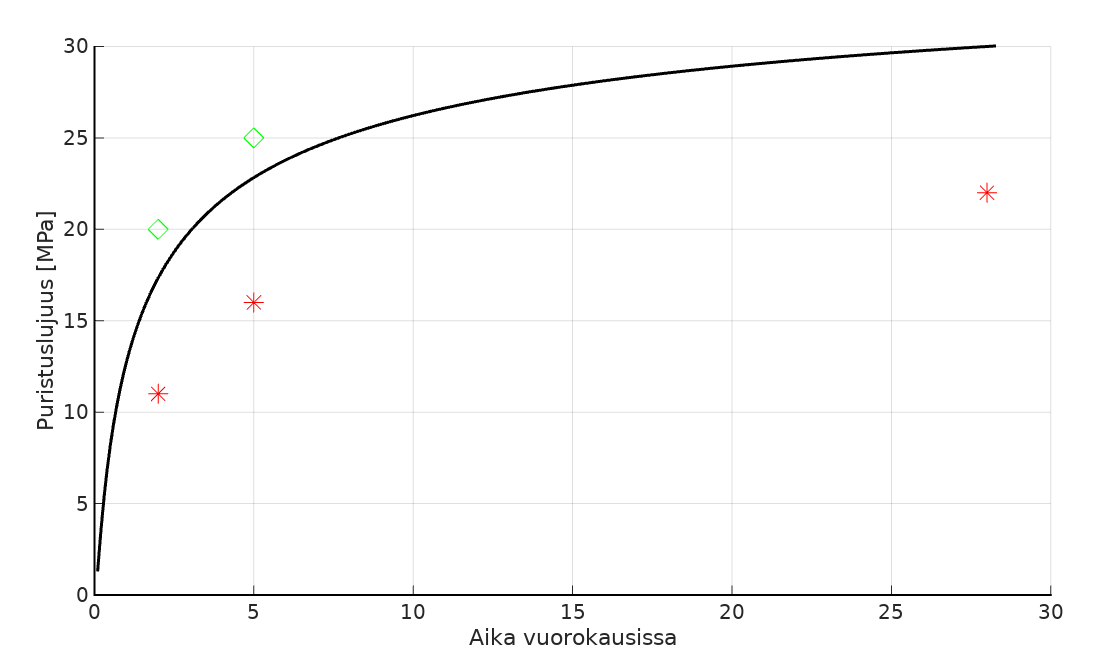
Matematiikassa on paljon puhuttu xy-tasosta. Miksi se on tärkeä? Juuri tämän kaltaisissa tilanteissa. Suuren mitatun aineiston mittauspisteet voidaan nyt piirtää xy-tasoon, ja nähdä, miten ne sijoittuvat tasolle. Tämä paljon puhuttu xy-taso, ja ymmärrys funktiosta, antaa siis insinöörimatemaatikolle työkalun, jolla ymmärretään yhden vaikuttavan tekijän vaikutusta johonkin tarkasteltavaan ilmiöön. Nyt vaikuttava tekijä on aika. Tietokannassa on siis tieto siitä, mikäsuuruisen puristuslujuuden betoni on saavuttanut kuivuttuaan tietyn määrän päiviä. Maalaisjärjellä tiedämme, että vuorokauden kuivunut betoni ei toki ole yhtä lujaa kuin puoli vuotta kuivunut, mutta insinöörillä täytyy olla tätä tarkkuutta parempi menetelmä arvioida, minkä vahvuista minkäkin ikäisen betonin pitäisi olla. Insinöörit ovat siis ottaneet kautta vuosien mittaustuloksensa ylös, ja nämä mittapisteet voidaan piirtää xy-tasoon, jossa x-koordinaatti on aika päivissä, ja y-koordinaatti on havaittu lujuus. Jälkipolville ei ole järkevää antaa referenssiksi koko tätä järjettömän suurta mittapisteiden joukkoa, vaan näihin mittapisteisiin sovitettu funktio. Kyseinen sovitefunktio on kuvassa alla.
Sovitefunktio, joka osuu mittapisteisiin parhaiten, on alla annettua muotoa. Kaavassa annettu vakio s voi saada sovelluksesta riippuen hieman eri arvoja, mutta sen tyypillinen arvo on s=0.2
Tuo yllä annettu funktio on siis sellainen, että se saavuttaa arvon 1, kun aikaa on kulunut 28 päivää. Insinöörit tietävät siis, että 28 päivässä puristuslujuus on saavuttanut maksimiarvonsa. Kun tuo annettu funktio kerrotaan tietyn betonilaadun lopullisella puristuslujuudella (käsittelemässämme tapauksessa 30 MPa), voidaan piirtää kuvaaja, joka kertoo kuivuvan betonin vaaditun puristuslujuuden tietyn ajan kuluttua valamisesta. Uusien valujen puristuslujuuksien arvojen pitäisi siis olla tämän käyrän yläpuolella.
Tässä vaiheessa voi tulla mieleen, miksi tämä on ollenkaan tärkeää. Eikö uusien betonivalujen voitaisi yksinkertaisesti antaa aina kuivua niin kauan, että se on saavuttanut suurimman puristuslujuutensa? Silloin voitaisiin unohtaa kaikki tämä ”tarpeeton” matematiikka. Tämä ei kuitenkaan ole käytännössä järkevää missään tilanteessa, koska rakentaja haluaa varmistua uuden betonin laadusta jo mahdollisimman aikaisin. Yrityselämässä aika on rahaa.
Katsotaan vielä kuvaa. Musta käyrä on siis SOVITEFUNKTIO siihen mittausdataan, joka vuosien aikana on saatu. Nyt, kun rakennusfirma tekee uutta betonivalua, se voi tehdä muutaman yksinkertaisen mittauksen, ja olla varma jo viidennen päivän kohdalla betovalun laadusta. Jos mitatut lujuudet ovat esimerkiksi punaisten pisteiden kohdalla, voimme olla varmoja, että betoni ei tule täyttämään vaadittuja kriteerejä. Jo viidennen päivän kohdalla voimme arvata, että lopullinen lujuus tulee olemaan jossakin niillä paikkeilla, jossa on punainen piste 28 vuorokauden päästä. Mittauksilla ja matemaattisella mallilla voimme siis ”ennustaa tulevaa”, nykyhetken dataan perustuen. Vastaavasti, jos mitatut lujuudet päätyvät vihreiden timanttien edustamiin arvoihin, tiedämme jo viidennen päivän kohdalla, että betonierä on onnistunut.