Àngulos entre vectores

Definicion.

Un vector es una cantidad que tiene una longitud (un número real no negativo), así como dirección (u orientación). Los vectores pueden ser representados en dos dimensiones, por ejemplo A = (Ax, Ay), y en tres dimensiones, A = (Ax, Ay, Az). Dos vectores A y B pueden están inclinados en un ángulo θ respecto uno del otro (Figura I); la forma más sencilla de determinar dicho ángulo, es calcular el arco coseno del producto escalar de ambos vectores dividido entre el producto de sus módulos: $\theta =\arccos \left (\frac{\vec{A}\cdot \vec{B}}{\left | \vec{A} \right |\left | \vec{B} \right |} \right )$

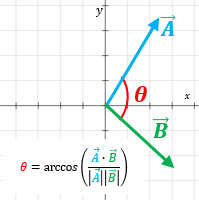
FÓRMULA PARA CALCULAR EL ÁNGULO ENTRE DOS VECTORES

El ángulo entre dos vectores A = (Ax, Ay, Az) y B = (Bx, By, Bz) se determina a partir de la siguiente fórmula: $\theta =\arccos \left (\frac{\vec{A}\cdot \vec{B}}{\left | \vec{A} \right |\left | \vec{B} \right |} \right )$ Donde:

AB es el producto escalar de A y B.
|A| y |B| son los módulos de cada vector.

PASOS PARA CALCULAR EL ÁNGULO ENTRE DOS VECTORES

Supongamos que se desea calcular el ángulo entre los vectores: $\begin{align*} \vec{A} &= (A_{x},A_{y},A_{z}) \\ \vec{B} &= (B_{x},B_{y},B_{z}) \end{align*}$

Calcular el producto escalar de ambos vectores:

$\vec{A}\cdot \vec{B}=A_{x}B_{x}+A_{y}B_{y}+A_{z}B_{z}$

Calcular (por separado) los módulos de ambos vectores:

$\left | \vec{A} \right |=\sqrt{\left ( A_{x} \right )^{2}+\left ( A_{y} \right )^{2}\left ( A_{z} \right )^{2}}$ $\left |\vec{B}\right |=\sqrt{\left ( B_{x} \right )^{2}+\left ( B_{y} \right )^{2}+\left ( B_{z} \right )^{2}}$

Sustituir los valores del paso 1 y paso 2 en la fórmula:

$\theta =\arccos \left (\frac{\vec{A}\cdot \vec{B}}{\left | \vec{A} \right |\left | \vec{B} \right |} \right )$

EJERCICIOS RESUELTOS

Calcular el ángulo entre los vectores:

$\begin{align*} \vec{A} &= (2,4) \\ \vec{B} &= (-2, 3) \end{align*}$ Calculamos el producto escalar de ambos vectores: $\vec{A}\cdot \vec{B}=(2)(-2)+(4)(3)=-4+7=3$ Calculamos los módulos de ambos vectores: $\begin{align*} \left |\vec{A}\right |&=\sqrt{( 2 )^{2}+(4)^{2}}= \sqrt{4+16}=\sqrt{20} \\ \left |\vec{B}\right |&=\sqrt{( -2 )^{2}+(3)^{2}= \sqrt{4+9}=\sqrt{13} } \end{align*}$ Sustituimos los resultados anteriores en la fórmula: $\begin{align*} \theta &=\arccos (\frac{6}{\sqrt{20}\sqrt{13}}) \\ &=\arccos (\frac{6}{\sqrt{260}}) \\ &= 1,18\hspace{0.3em}rad \end{align*}$ Como 1 radian ≅ 57.296 °, entonces: $\theta =67,6^{\circ}$

Calcular el ángulo entre los vectores:

$\begin{align*} \vec{A} &= (-1,3,4) \\ \vec{B} &= (5,-2,7) \end{align*}$ Calculamos el producto escalar de ambos vectores: $\vec{A}\cdot \vec{B}=(-1)(5)+(3)(-2)+(4)(7)=-5-6+28=17$ Calculamos los módulos de ambos vectores: $\begin{align*} \left |\vec{A}\right |&=\sqrt{( -1 )^{2}+(3)^{2}+(4)^{2}}= \sqrt{1+9+16}=\sqrt{26} \\ \left |\vec{B}\right |&=\sqrt{( 5 )^{2}+(-2)^{2}+(7)^{2}= \sqrt{25+4+49}=\sqrt{78} } \end{align*}$ Sustituimos los resultados anteriores en la fórmula: $\begin{align*} \theta &=\arccos (\frac{17}{\sqrt{26}\sqrt{78}}) \\ &=\arccos (\frac{17}{\sqrt{2028}}) \\ &= 1,562\hspace{0.3em}rad \end{align*}$ Como 1 radian ≅ 57.296 °, entonces: $\theta =89,5^{\circ}$

Àngulos entre vectores

Definicion.

FÓRMULA PARA CALCULAR EL ÁNGULO ENTRE DOS VECTORES

PASOS PARA CALCULAR EL ÁNGULO ENTRE DOS VECTORES

EJERCICIOS RESUELTOS

Novi radovi

Istraži uratke

Otkrij teme