Puntos de una recta
Puntos que pertenecen a una recta
Para determinar de manera algebraica si un punto pertenece a una recta, basta con comprobar si al sustituir las
coordenadas (x, y) del punto en la ecuación de la recta se obtiene un resultado consistente.
Por ejemplo, el punto (2,7) pertenece a la recta y = 2x + 3 ya que si sustituimos x=2, y=3
en la ecuación de la recta se obtiene
7 = 2(2) + 3
7 = 7
por tanto el punto pertenece a la recta.
En cambio, el punto (1,3) no pertenece a la recta y = 2x + 3 ya que
3 = 2(1) + 3
3 5
Actividad 1
Seleccionar los puntos que pertenezcan a la recta y = 3x − 2
De manera gráfica, todos los puntos que pertenecen a una recta deben estar alineados con ella.
Dos puntos importantes de una recta son los cortes con los ejes. El corte con el eje x, es el punto de la recta para el que y=0, mientras que el corte con el eje y se corresponde para el punto de la recta para el que x=0.
Por ejemplo, en la recta y=2x+3, el corte con el eje x se obtiene haciendo y=0
0=2x+3
por lo que x=-3/2, y el punto de corte con el eje x es (-3/2,0)
El corte con el eje y se obtiene haciendo x=0, por tanto
y=2(0)+3
por lo que y=3 y el punto de corte con el eje y es (0,3)
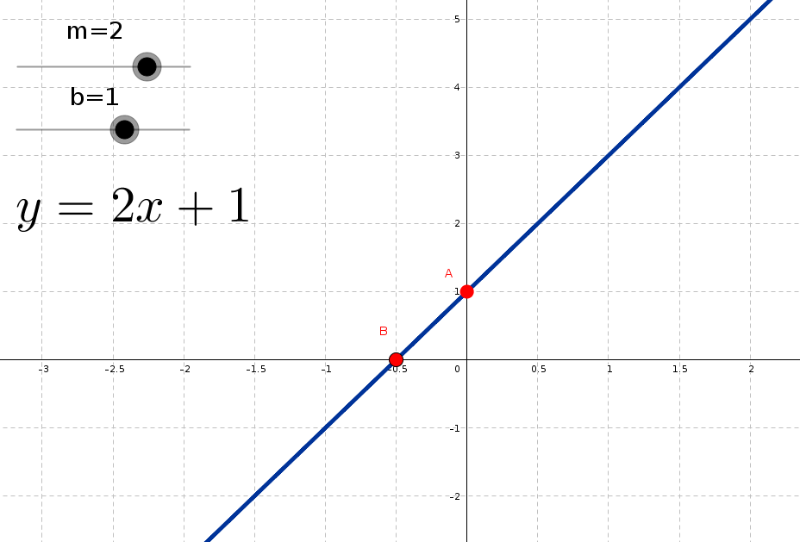
En la siguiente hoja dinámica se puede comprobar de manera gráfica los puntos de corte de una recta. El punto A es el corte con el eje y mientras que el punto B es el corte con el eje x. Moviendo los puntos se obtiene la ecuación de la recta que pasa por ellos.
Actividad 2
Calcular los puntos de corte de la recta y=4x+2. Comprobar la respuesta usando la hoja dinámica