Google Classroom
GeoGebraAula GeoGebra
GeoGebra

Quina dimensió tenen?

Autor:Jordi Campos Miralles

Esmenta tres exemples d'objectes que siguin 2D i tres exemples d'objectes que siguin 3D:

Com es relacionen les dimensions?

Observa la imatge següent:
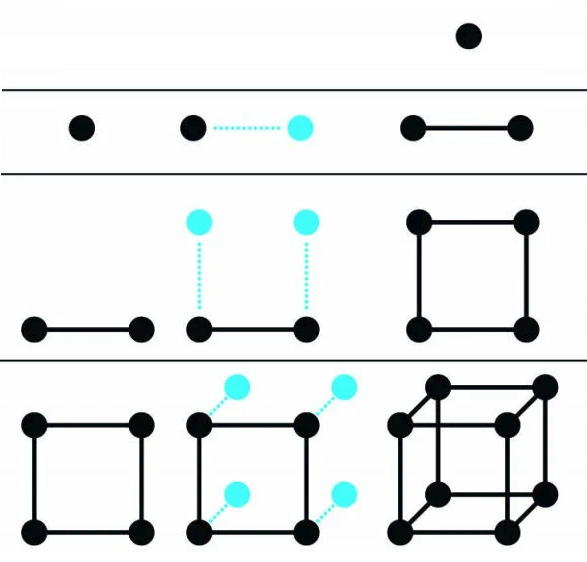
Image
Fixa't que:
  • "Dins" d'un punt ideal no hi ha espai per moure's, té zero dimensions 0D (a la imatge hi ha dibuixat un cercle en comptes d'un punt sense dimensió, ja que no el veuríem).
  • Si arrossegues el punt en "una direcció" passes a tenir un segment que té 1D.
  • Si arrossegues tots els punts del segment en "una direcció diferent de l'usada per crear-lo" passes a tenir un quadrat, 2D.
  • Si arrossegueus tots els punts del quadrat en "una direcció diferent de l'usada per crear-lo" passes a tenir un cub, 3D.

Què passa quan faig més gran els objectes?

Mira què passa en segment, el quadrat i el cub quan els escalo per 2 (faig els seus costats el doble de llargs):
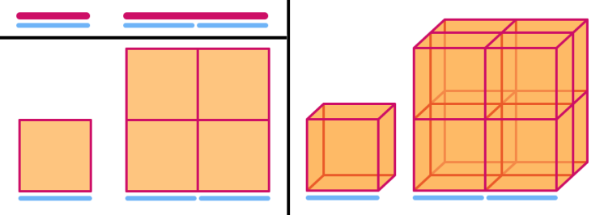
Image

1D: Quan escalo el segment original per 2, quantes vegades podries dir que es repeteix?

Marqueu on calgui
  • A
  • B
  • C
  • D
  • E
Comprova la meva reposta (3)

2D: Quan escalo el quadrat original per 2, quantes vegades podries dir que es repeteix?

Marqueu on calgui
  • A
  • B
  • C
  • D
  • E
Comprova la meva reposta (3)

3D: Quan escalo el quadrat original per 2, quantes vegades podries dir que es repeteix?

Marqueu on calgui
  • A
  • B
  • C
  • D
  • E
Comprova la meva reposta (3)

Com puc calcular la dimensió d'un objecte?

1D: Veuràs que en multiplicar per 2 l'extensió del segment que és d'1 dimensió, acabem tenint 2 vegades el segment original: 2¹ = 2. 2D: Veuràs que en multiplicar per 2 l'extensió del quadrat que és de 2 dimensions, acabem tenint 4 vegades el segment original: 2² = 4.

3D: Fes una explicació com les anteriors pel cas del cub, incloent-hi l'expressió de càlcul que relaciona el canvi a l'extensió, amb les dimensions i les vegades que es repeteix.

Quina dimensió té el Triangle de Sierpinski?

Usarem el mètode anterior per calcular la dimensió d'aquesta fractal:
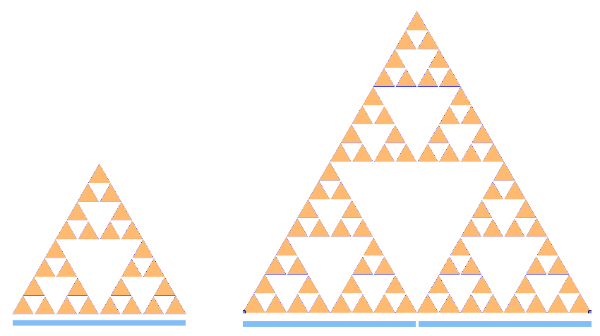
Image

Quan escalo el Triangle de Sierpinski original per 2, quantes vegades podries dir que es repeteix?

Marqueu on calgui
  • A
  • B
  • C
  • D
  • E
Comprova la meva reposta (3)
De manera que podem escriure la relació següent: 2? = 3. És a dir, que quan he multiplicat per 2 l'extensió del triangle de Sierpinski l'he acabat tenint 3 vegades. Així que puc calcular quin nombre hauria de posar al lloc de l'actual ? dimensions que correspondrà justament a les dimensions que té el triangle. Resulta que:
  • si la dimensió fos 1, aleshores 21 = 2 és massa petit.
  • si la dimensió fos 2, aleshores 22 = 4 és massa gran.
I per tant deu d'estar entremig. En matemàtiques jo puc saber "a quin número he d'elevar 2 perquè em doni 3" a través de la funció logaritme la qual cosa significa que:
  • la dimensió del Triangle de Sierpinski és aproximadament 1,585 ja que 21,585 = 3.
De fet, precisament d'aquí és d'on va sortir el nom de fractal, del fet que no tenen una dimensió entera (1D, 2D, 3D...) sinó que és una fracció (ex. 1,585 en aquest cas, però altres fractals tenen altres dimensions).

Fonts d'informació i imatges:

Internal, What is a fractal - https://iternal.us/what-is-a-fractal/ Mathigon, Fractales - https://es.mathigon.org/course/fractals/

Nous materials

Descobriu materials

Descobriu Temes