Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

Enhetssirkelen

Autor:Eva Holthe Enoksen
Frem til nå har vi brukt en rettvinklet trekant for å definere sinus, cosinus og tangens. Dette har sine begrensninger, så i dag skal vi lære en mer og generell definisjon. Men først: Repetisjon
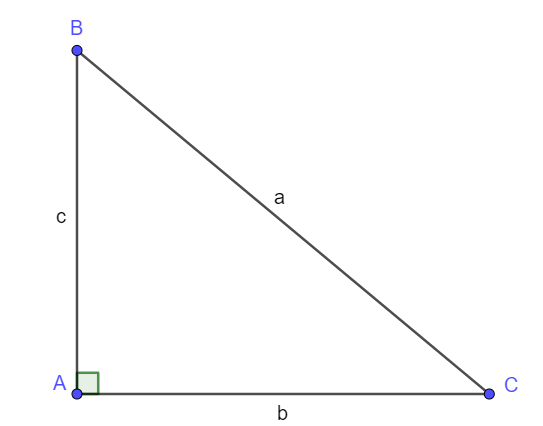
Image

Oppgave 1

Hva er hosliggende katet til vinkel C?

Marca todas las que correspondan
  • A
  • B
  • C
Revisa tu respuesta (3)

Oppgave 2

Skriv opp uttrykkene for sin(C), cos(C) og tan(C) basert på trekanten over

Over ser vi en sirkel med et punkt P på sirkelbuen med koordinatene. Vi ser at vinkelen v er vinkelen mellom x-aksen og linja fra origo til punktet. Vi får også oppgitt x- og y-koordinatene til P. Sirkelen har radius 1, og kalles derfor for enhetssirkelen.

Oppgave 3

Dra i spaken for å justere vinkelen v. Beskriv hva som skjer med punktet P.

Oppgave 4

Juster P slik at Bruk sirkelen til å finne sin(v) og cos(v). Hint: Hva vet du om hypotenusen i trekanten?

Revisa tu respuesta

Oppgave 5

Hva er riktig om koordinatene til punktet P?

Marca todas las que correspondan
  • A
  • B
  • C
Revisa tu respuesta (3)

Oppgave 6

Dra nå i v slik at vinklene blir større enn 90 grader. Beskriv hva som skjer nå.

Oppgave 7

Det finnes nå to vinkler der sin(v)=0.5. Den ene kjenner du godt til. Finn den andre.

Revisa tu respuesta

Oppgave 8

Bruk enhetssirkelen til å finne cos(120)

Revisa tu respuesta

Oppgave 9

Finnes det mer enn en vinkel som har cos(v)=0.5. Hvorfor (ikke)?

Oppgave 10

Bruk Pytagoras' setning til å forklare/vise at

Ferdig?

Gjør oppgaver i Munchboka: https://reneaas.github.io/matematikk_1t/book/trigonometri/enhetssirkelen/oppgaver.html

Marca todas las que correspondan
  • A
  • B
Revisa tu respuesta (3)

Nuevos recursos

Descubrir recursos

Descubre temas