Áttekintés
₄Point Location estimators: Geometric Centers on a sphere
ΛM -Lagrange Multipliers with One Constraint. Finding Estimators of location on a surface of the sphere as Critical points of the corresponding Lagrangian for a discrete set of points.
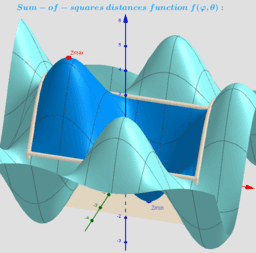
Expanded definition of the Geometric Centers https://en.wikipedia.org/wiki/Centroid as a point located in a restricted area and which not only minimizes, but also maximizes or is a saddle point for the sum of the squares of the distances function is.
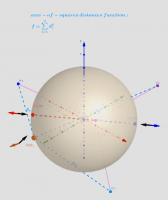
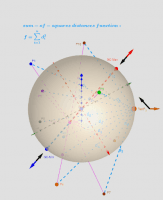
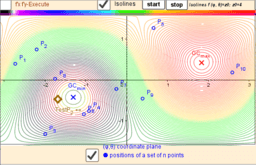
Let lP {P1,P2,...,Pn} -set of n points, {(xi,yi,zi)∈ℝ³: i = 1,...,n} -their coordinates is. The Geometric Centers on a bounded area (e.g. sphere S) are defined as points GC on this surface from where the function of sum of the squares of the distances to each point Pi's are critical points: local minimums, maximums or saddle points.
Critical points can be found using Lagrange multipliersas finding the Extreme values of the function f(x,y,z) subject to a constraining equation g(x,y,z)=x²+y²+z²-R². There is a system of equations: ∇f(x,y,z)= λ∇g(x,y,z). A local optimum occurs when ∇f(x,y,z) and ∇g(x,y,z) are parallel, and so ∇f is some multiple of ∇g.
In this problem there are only two critical points P=(x,y,z)∈S. The Axis passing through the radius vector of the point Sum(lP) passes through the center of mass Cm and intersects the spherical surface S at two points: one corresponds to the global maximum, the other- to the global minimum. Their coordinates have explicit formulas: GCmin= R* UnitVector(Sum(lP)) and GCmax= - R*UnitVector(Sum(lP)) - two antipodal points on the surface of a sphere. These points can be found using the Steiner theorem too.
ΛM 2d: Location estimators on a circle for a set of points -https://www.geogebra.org/m/u7zq6f3e
*From Book: Extended definitions of point location estimates https://www.geogebra.org/m/hhmfbvde
From: List of My Public Books on GeoGebra Topics: Constructing polyhedra -https://www.geogebra.org/m/eabstecp