GeoGebra

Vierecke

Autor:J.M.

Haus der Vierecke + Eigenschaften

Dies ist eine Übersicht über alle Vierecke, die es gibt. Unten, im Fundament findest du das einfachste Viereck. Alle anderen darüber sind auch Vierecke. Umgekehrt gilt dies aber nicht: Ganz oben siehst du das Quadrat, das man auch mit allen anderen Begriffen beschreiben kann. Aber das kann man nur beim Quadrat machen.
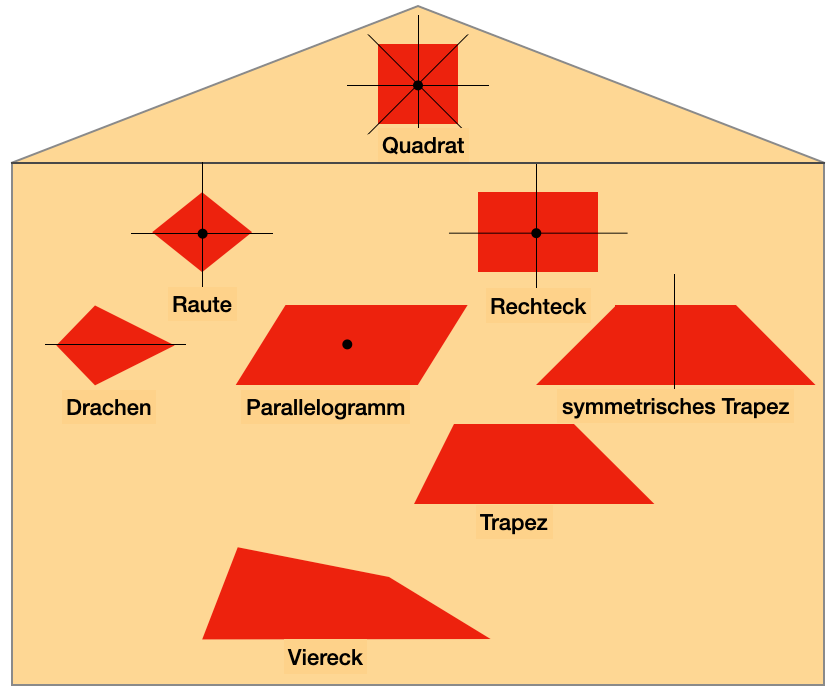
Hier siehst du die Übersicht, aber es sind hier noch die Symmetrien eingezeichnet. Es gibt die Punktsymmetrie und die Achsensymmetrie bei Vierecken.
Hier siehst du die Übersicht, aber es sind hier noch die Symmetrien eingezeichnet. Es gibt die Punktsymmetrie und die Achsensymmetrie bei Vierecken.

Haus der Vierecke - dynamisch

Quadrat

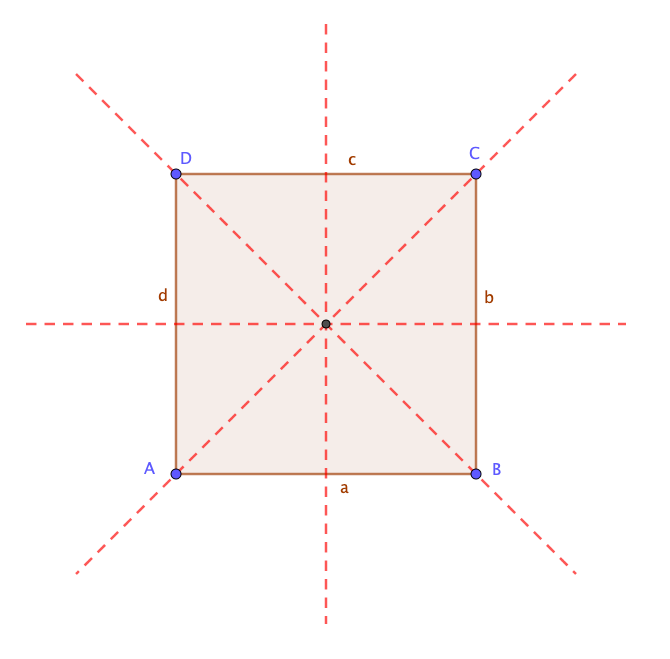
Quadrat
Hier siehst du die Übersicht, aber es sind hier noch die Symmetrien eingezeichnet. Es gibt die Punktsymmetrie und die Achsensymmetrie bei Vierecken.
[size=85][table][tr][td] Seiten[/td][td]alle vier Seiten sind gleich lang[/td][/tr][tr][td] Winkel[/td][td]vier rechte Winkel (90°)[/td][/tr][tr][td] Diagonalen[/td][td]gleich lange Diagonalen, die sich gegenseitig halbieren und senkrecht (90°) aufeinander stehen[/td][/tr][tr][td] Symmetrie[/td][td]Punktsymmetrie und Achsensymmetrie[/td][/tr][/table] Umfang:[/size] [math]u=a+b+c+d[/math] [math]u=4a[/math] [size=85]Flächeninhalt:[/size] [math]A=a\cdot a=a^2[/math]
 Seitenalle vier Seiten sind gleich lang
 Winkelvier rechte Winkel (90°)
 Diagonalengleich lange Diagonalen, die sich gegenseitig halbieren und senkrecht (90°) aufeinander stehen
 SymmetriePunktsymmetrie und Achsensymmetrie
Umfang: Flächeninhalt:

Rechteck und Quadrat

Rechteck

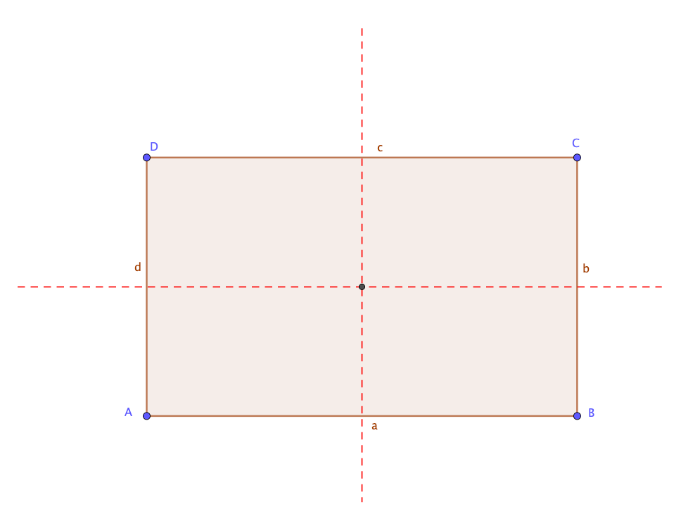
Rechteck
[size=85][table][tr][td] Seiten[/td][td]gegenüber liegende Seiten sind gleich lang[/td][/tr][tr][td] Winkel[/td][td]vier rechte Winkel (90°)[/td][/tr][tr][td] Diagonalen[/td][td]gleich lange Diagonalen, die sich gegenseitig halbieren [/td][/tr][tr][td] Symmetrie[/td][td]Punktsymmetrie und Achsensymmetrie[/td][/tr][/table] Umfang: [math]u=a+b+c+d[/math] [math]u=2a+2b[/math] [math]u=2(a+b)[/math] Flächeninhalt: [math]A=a\cdot b[/math][/size]

 Seitengegenüber liegende Seiten sind gleich lang
 Winkelvier rechte Winkel (90°)
 Diagonalengleich lange Diagonalen, die sich gegenseitig halbieren
 SymmetriePunktsymmetrie und Achsensymmetrie
Umfang: Flächeninhalt:
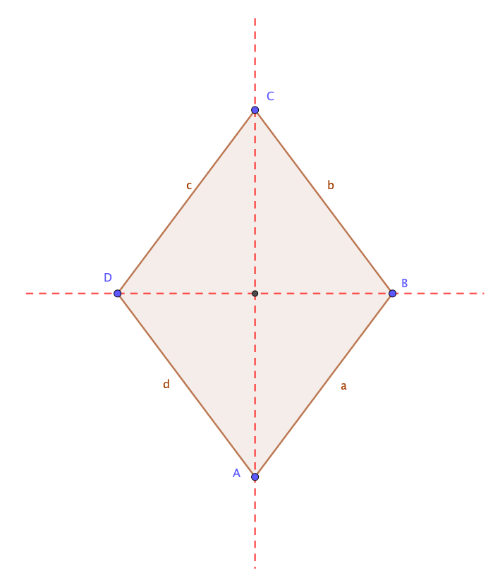
Image
[size=85][table][tr][td] Seiten[/td][td]alle vier Seiten sind gleich lang[/td][/tr][tr][td] Winkel[/td][td]gegenüber liegende Winkel sind gleich groß[/td][/tr][tr][td] Diagonalen[/td][td]Diagonalen halbieren sich gegenseitig und senkrecht (90°) aufeinander stehen [/td][/tr][tr][td] Symmetrie[/td][td]Punktsymmetrie und Achsensymmetrie [/td][/tr][/table] Umfang: [math]u=a+b+c+d[/math] [math]u=2(a+b)[/math] Flächeninhalt: [math]A=\frac{1}{2}e\cdot f[/math][/size]
 Seitenalle vier Seiten sind gleich lang
 Winkelgegenüber liegende Winkel sind gleich groß
 DiagonalenDiagonalen halbieren sich gegenseitig und senkrecht (90°) aufeinander stehen
 SymmetriePunktsymmetrie und Achsensymmetrie
 Umfang: Flächeninhalt:
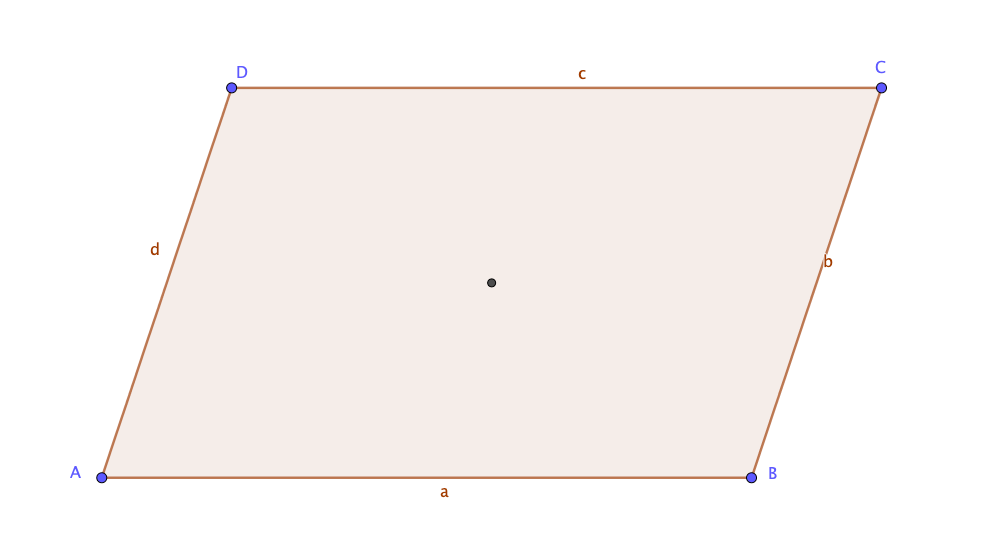
Image
[size=85][table][tr][td]Seiten  [/td][td]gegenüber liegende Seiten sind gleich lang und parallel [/td][/tr][tr][td]Winkel[/td][td]gegenüber liegende Winkel sind gleich groß[/td][/tr][tr][td]Diagonalen[/td][td]Diagonalen halbieren sich gegenseitig [/td][/tr][tr][td]Symmetrie[/td][td] Punktsymmetrie[/td][/tr][/table] Umfang: [math]u=a+b+c+d[/math] [math]u=2(a+b)[/math] Flächeninhalt: [math]A=a\cdot ha[/math] [/size]
Seiten  gegenüber liegende Seiten sind gleich lang und parallel
Winkelgegenüber liegende Winkel sind gleich groß
DiagonalenDiagonalen halbieren sich gegenseitig
Symmetrie Punktsymmetrie
 Umfang: Flächeninhalt:
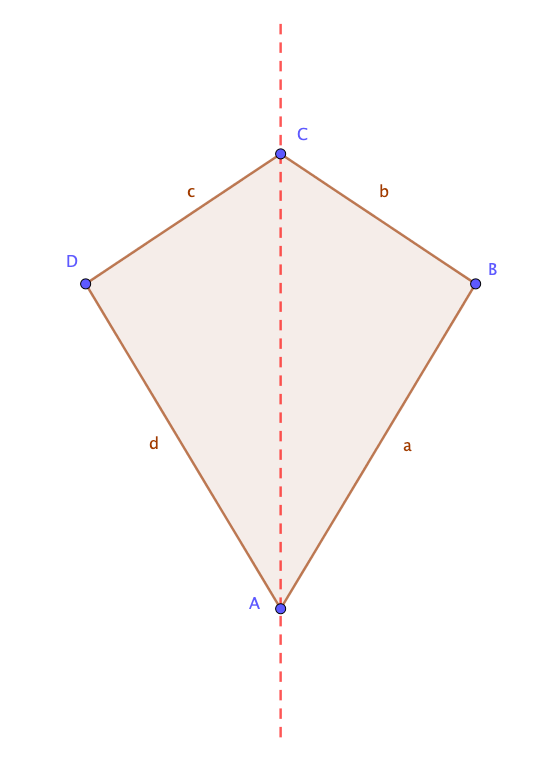
Image
[size=85][table][tr][td]Seiten[/td][td]zwei Paare benachbarter Seiten sind gleich lang[/td][/tr][tr][td]Winkel[/td][td]zwei gegenüber liegende Winkel sind gleich groß (zwei nicht!)[/td][/tr][tr][td]Diagonalen[/td][td]Diagonalen stehen senkrecht (90°) aufeinander [/td][/tr][tr][td]Symmetrie[/td][td] Achsensymmetrie[/td][/tr][/table] Umfang: [math]u=a+b+c+d[/math] [math]u=2(a+b)[/math] Flächeninhalt: [math]A=\frac{1}{2}e\cdot f[/math][/size]
Seitenzwei Paare benachbarter Seiten sind gleich lang
Winkelzwei gegenüber liegende Winkel sind gleich groß (zwei nicht!)
DiagonalenDiagonalen stehen senkrecht (90°) aufeinander
Symmetrie Achsensymmetrie
 Umfang: Flächeninhalt:
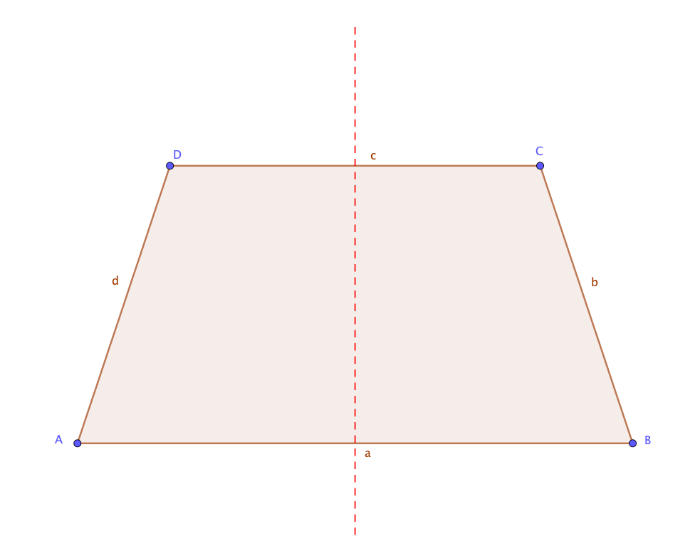
Image
[size=85][table][tr][td]Seiten  [/td][td]wei gegenüberliegende Seiten sind parallel, die anderen gegenüber liegenden Seiten sind gleich lang [/td][/tr][tr][td]Winkel[/td][td]wei Paar gleich große benachbarte Winkel, gegenüberliegende Winkel sind in der Summe 180° groß[/td][/tr][tr][td]Diagonalen[/td][td]Diagonalen sind gleich lang[/td][/tr][tr][td]Symmetrie[/td][td] Achsensymmetrie[/td][/tr][/table] Umfang: [math]u=a+b+c+d[/math] Flächeninhalt: [math]A=\frac{1}{2}(a+c)\cdot h[/math][/size]
Seiten  wei gegenüberliegende Seiten sind parallel, die anderen gegenüber liegenden Seiten sind gleich lang
Winkelwei Paar gleich große benachbarte Winkel, gegenüberliegende Winkel sind in der Summe 180° groß
DiagonalenDiagonalen sind gleich lang
Symmetrie Achsensymmetrie
 Umfang: Flächeninhalt:
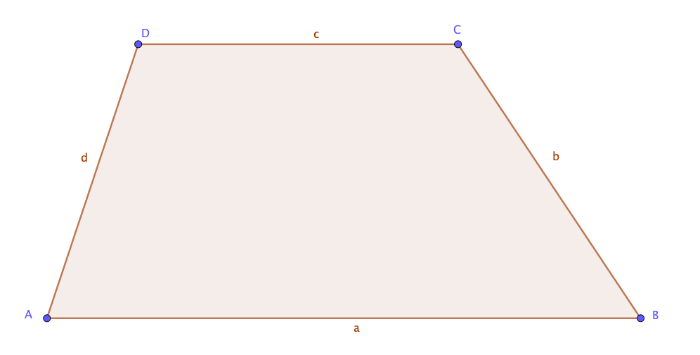
Image
[size=85][table][tr][td]Seiten  [/td][td]zwei Seiten sind parallel[/td][/tr][tr][td]Winkel[/td][td]vier unterschiedliche Winkel[/td][/tr][tr][td]Diagonalen[/td][td]zwei Diagonalen, keine Besonderheit[/td][/tr][tr][td]Symmetrie[/td][td] keine[/td][/tr][/table] Umfang: [math]u=a+b+c+d[/math] Flächeninhalt: [math]A=\frac{1}{2}(a+c)\cdot h[/math][/size]
Seiten  zwei Seiten sind parallel
Winkelvier unterschiedliche Winkel
Diagonalenzwei Diagonalen, keine Besonderheit
Symmetrie keine
Umfang: Flächeninhalt:
[size=85][table][tr][td]Seiten[/td][td]alle vier Seiten sind meist verschieden[/td][/tr][tr][td]Winkel[/td][td]meist vier unterschiedliche Winkel[/td][/tr][tr][td]Diagonalen[/td][td]zwei Diagonalen, keine Besonderheit[/td][/tr][tr][td]Symmetrie[/td][td]keine[/td][/tr][/table] Umfang: [math]u=a+b+c+d[/math] Flächeninhalt: Nicht direkt berechenbar![/size]
Seitenalle vier Seiten sind meist verschieden
Winkelmeist vier unterschiedliche Winkel
Diagonalenzwei Diagonalen, keine Besonderheit
Symmetriekeine
 Umfang: Flächeninhalt: Nicht direkt berechenbar!

Neue Materialien

Entdecke Materialien

Entdecke weitere Themen