Potencias de un número complejo
Una vez introducido nuestro número complejo podemos experimentar con sus potencias naturales, es decir, .
Guía de construcción
- Escribimos en la barra de entrada: 1 + i (aparecerá el nombre z1)
- Creamos un deslizador de tipo entero con los parámetros por defecto. Por defecto lo llama n.
- Usamos el comando secuencia para crear las potencias naturales de z1. . Escribimos en la barra de entrada:
potencias=Secuencia[z_1^k,k,1,n]
Con esta sencilla construcción, que ampliaremos a lo largo del artículo, ya podemos observar qué sucede con las potencias de exponente natural de un número complejo. Si activamos la vista algebraica, veremos una lista con las potencias del número complejo. En la vista gráfica veremos los puntos correspondientes y ahí es donde empieza nuestra investigación. Si movemos el punto z1 observaremos como varían las potencias. De forma casi automática tanto a profesores como a alumnos nos asalta la pregunta ¿qué patrón siguen las sucesivas potencias?
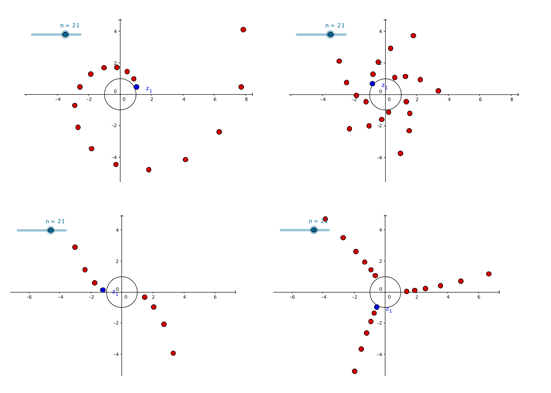
Rápidamente sacamos un conclusión, la “figura” que describen los puntos depende de al menos el módulo del número complejo.
En este punto vamos a unir con segmentos las potencias consecutivas, es decir, los segmentos, y también representaremos la circunferencia unidad en un intento de ver qué sucede
Guía de construcción
- En el fichero anterior, escribimos en la barra de entrada:
- Circunferencia[(0,0),1]
- linea= Poligonal[potencias]
- Añadimos una casilla de control para ocultar/mostrar la línea poligonal creada en la guía anterior.