Libro de porcentaje
Inicio
Enseñaremos porcentaje a través de un juego de ruleta de
aumentos y descuentos de un supermercado.
Explicación del juego:
Se les muestra la ruleta y se les explica que los
porcentajes que aparecen en ella representan aumentos o descuentos. Por
ejemplo, si la ruleta cae en el + 10%, significa que el precio del producto
aumentará un 10%.
Se procede a armas
grupos de 4 integrantes a donde se les entregara una tarjeta que contenga un
precio de un producto del supermercado.
Cada alumno girara la ruleta y según el porcentaje que les
toque deberán calcular a cuanto se va el precio del producto, dependiendo si es
un descuento o aumento.
Desarrollo
Situaciones problemáticas como ejemplo
-Si a María le toca una tarjeta de productos de limpieza que
tiene un valor de $500 y al girar la ruleta le toca + 40% ¿Cuánto será el valor
final de los productos aplicando ese aumento?
-Si a Pedro al girar la ruleta le toca un -15% y en su
tarjeta los productos de higiene personal tienen un valor de $1.200 ¿Cuánto
será el valor final de los productos aplicando ese descuento?
Cada grupo deberá tener 4 valores distintos de porcentajes,
trabajarlos y verificar sus resultados interactuando entre los grupos.
Presentadas las situaciones nos preguntamos:
-¿Cómo se calcula el porcentaje?
-¿Qué relación tiene el porcentaje con la fracción?
Cierre:
Como actividad de cierre se propone
plantear las siguientes preguntas:
¿Qué es el porcentaje y para que
nos sirve en la vida cotidiana?
¿Por qué crees que los comerciantes
cobran un 10% de recargo con las compras con tarjeta de crédito?
Utilizamos las tarjetas de forma interactiva
Formas de Jugar con una ruleta creada en Geogebra
¡JUGAMOS A LA RULETA! Tendremos un aumento o un descuento? ¡A JUGAR! ¡SUERTE!
Imaginemos que vamos a comprar una computadora que cuesta $150.000. El IVA actual en Argentina es del 21% ¿Cuánto representa el IVA?
Juguemos a los calculos mentales, elige la opcion que consideres valida
Cuanto es el 25% de 300?
Cuanto es el 60% de 1500?
Cuanto es el 150% de 3000?
Cuanto es el 40% de 20?
Cuanto es el 15% de 50?
Parte Conceptual
¿Qué es un porcentaje?En matemáticas y estadística, se llama porcentaje a la expresión de una cantidad determinada como una fracción de cien (100) partes iguales. Dicho más fácilmente, el porcentaje es la relación de proporcionalidad entre dos unidades o entre una unidad y un conjunto de ellas, expresado en términos de x por cada 100 unidades, es decir, de tanto por ciento (literalmente: tanto por cada ciento o cada centena).Convencionalmente, el porcentaje se expresa con el signo %, acompañando a la cifra del porcentaje: 25 % (un cuarto), 50 % (la mitad) o 100 % (todo). Por lo tanto, con este tipo de expresiones matemáticas se puede indicar cuánto representa una cifra de otra o del total de un conjunto de elementos.Por ejemplo, si tenemos en una bolsa cien manzanas, esa cifra total representa el 100 % de las manzanas (o sea, 100 manzanas de cada 100); si regalamos cincuenta manzanas a un amigo (50 de cada 100 manzanas iniciales) nos quedaremos entonces con el 50 % de lo que teníamos, es decir, la mitad; y si de esa mitad resultan estar dañadas 25 manzanas (25 de cada 100 manzanas iniciales), acabaremos únicamente con 25 % de la cifra inicial, es decir, un cuarto del total.Los porcentajes son sumamente útiles para expresar proporciones y comparar unas fracciones con otras. ¿Cómo calcular un porcentaje?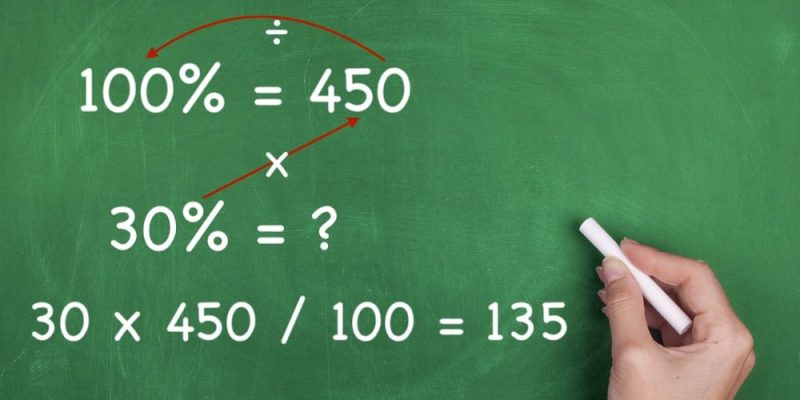
La regla de tres facilita el cálculo de los porcentajes.Para calcular el porcentaje de un número debemos multiplicar la cifra por el porcentaje deseado y dividirlo todo entre 100. Por ejemplo, si queremos saber cuánto es el 30 % de 450, basta con que multipliquemos 30 x 450 y dividamos el resultado entre 100, lo cual arroja que el 30 % de 450 es 135.Otra forma de plantear esta operación es establecer una regla de 3, de la siguiente manera:dado que el 100 % es 450entonces el 30 % es XPara despejar la incógnita (x), debemos multiplicar en diagonal (30 x 450) y dividir en horizontal (entre 100). Esto significa que x = (30 x 450) / 100, o sea, x = 135.
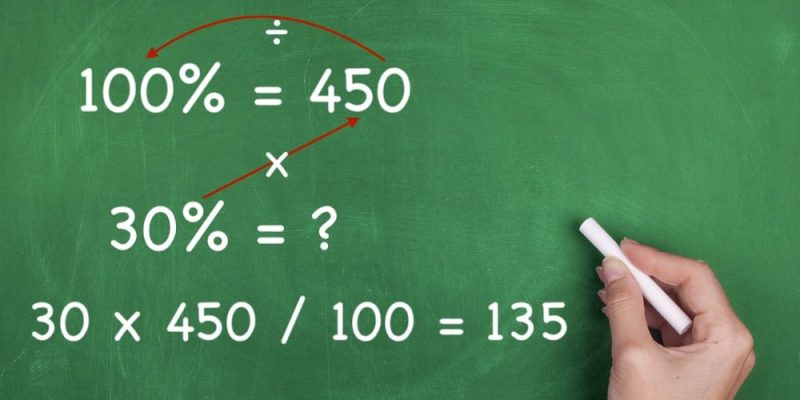La regla de tres facilita el cálculo de los porcentajes.Para calcular el porcentaje de un número debemos multiplicar la cifra por el porcentaje deseado y dividirlo todo entre 100. Por ejemplo, si queremos saber cuánto es el 30 % de 450, basta con que multipliquemos 30 x 450 y dividamos el resultado entre 100, lo cual arroja que el 30 % de 450 es 135.Otra forma de plantear esta operación es establecer una regla de 3, de la siguiente manera:dado que el 100 % es 450entonces el 30 % es XPara despejar la incógnita (x), debemos multiplicar en diagonal (30 x 450) y dividir en horizontal (entre 100). Esto significa que x = (30 x 450) / 100, o sea, x = 135.