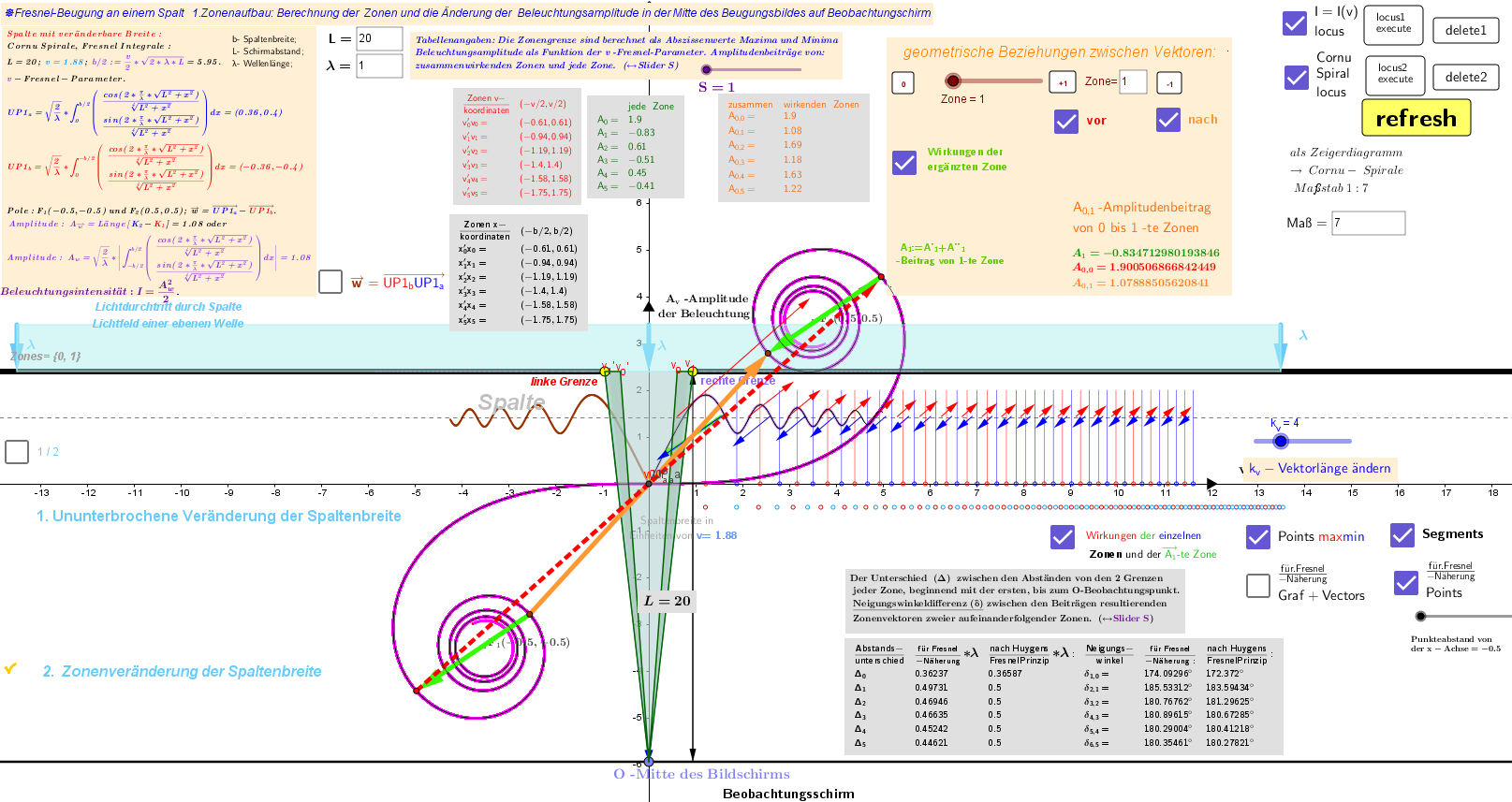
Untersuchung der Änderung der Beugungsintensität auf der Spaltachse mit sukzessiver Vergrößerung der Spaltbreite. Das Beugungsintegral wird nach dem Huygens-Fresnel-Prinzip berechnet.
Das vorliegende Applet ist eine erweiterte Version des Applets und ähnelt dem Applet, das den Fall der Fresnel-Näherung berücksichtigt.
Vergrößern Sie konsequent die Spaltenbreite, die im Applet als verallgemeinerter Parameter v:=b/sqrt(2*λ*L) behandelt wird (b -tatsächliche Spaltenbreite, λ -Wellenlänge und L -Schirmabstand). In der Mitte des Bildschirms, der sich in einer bestimmten L -Entfernung befindet, ändert sich die A -Amplitude der resultierenden Schwingung, die mit dem entsprechenden Beugungsintegral berechnet wird (F (w) = C (w) + iS(w) -Fresnel-Integral), in einer oszillierenden Weise. {v1, v2, ...} eine Folge von Extremwerten, die als v-Zonengrenzen betrachtet werden.
Mit dem Applet können Sie den Aufbau von "Fresnel"-Zonen bei der Beugung am Spalt untersuchen. Zur Veranschaulichung wird ein Vektordiagramm erstellt - die sogenannte Cornu-Spirale (Klothoide). Sie kann dazu verwendet werden, den Beitrag der einzelnen Zonen und den Prozess der "Bildung" der resultierenden Amplitude zu untersuchen.
Fall → ☑1/2: 1. Ununterbrochene Veränderung der Spaltbreite.
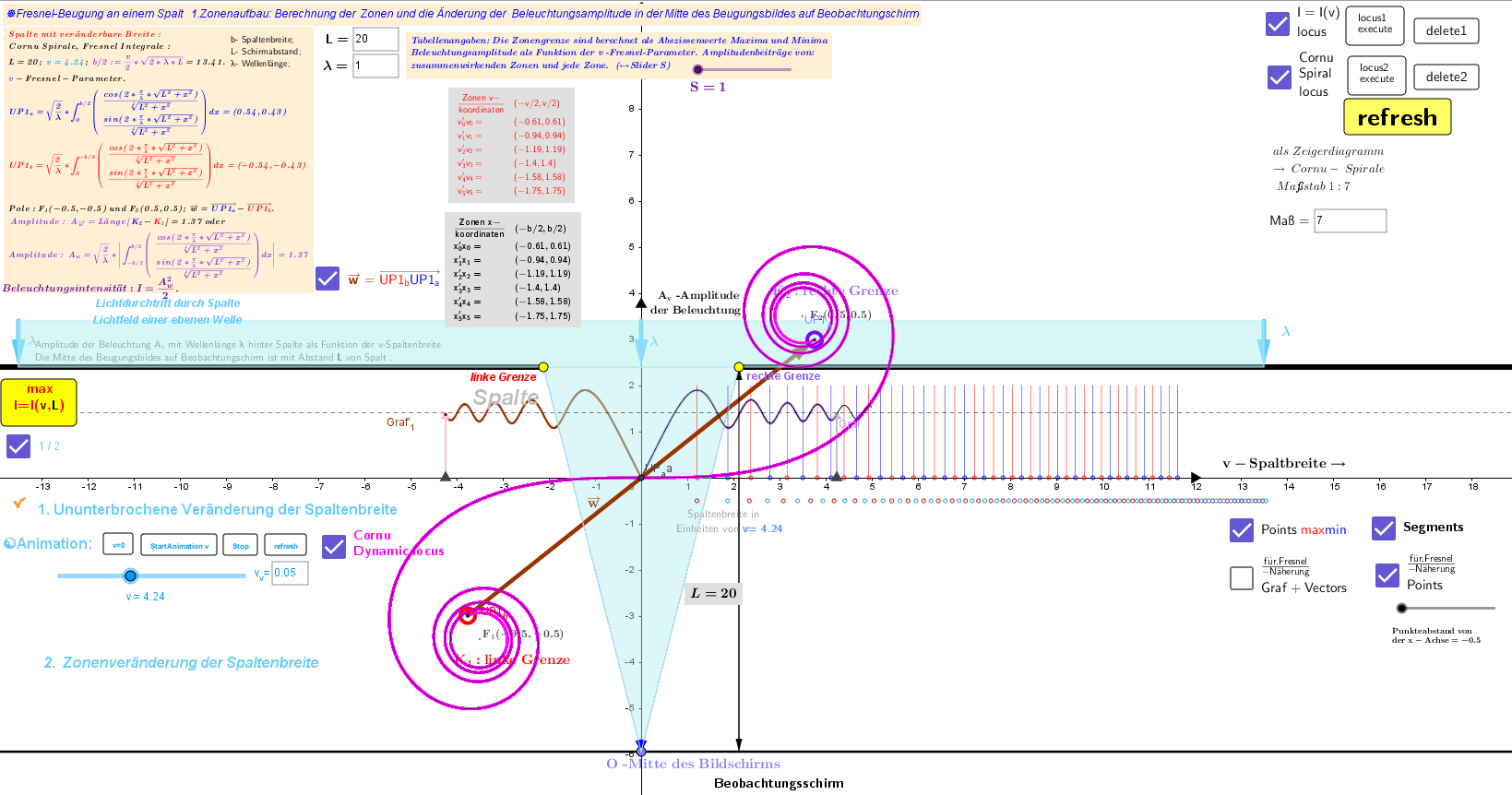
Fall → ☐ 1/2: 2. Veränderung der Spaltbreite Zonenweise.