Calissons
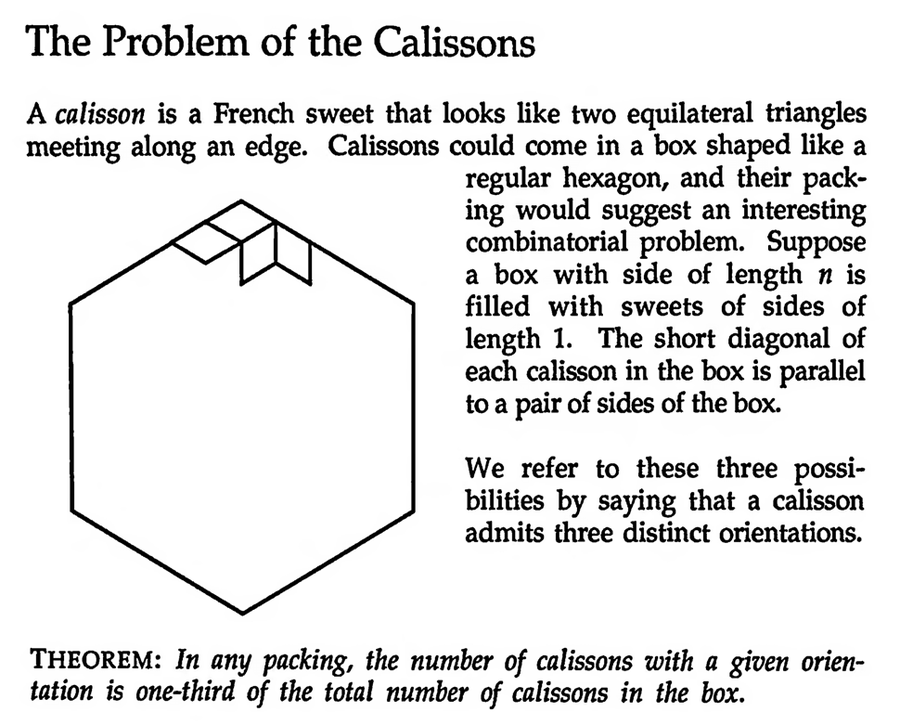
Considérons un calisson comme 2 triangles équilatéraux collés par un côté. Si on range les calissons de côté 1 dans une boite hexagonale de côté n, il y a 3 orientations possibles.
Montrer qu'il y a autant de calissons dans chacune des orientations.
Par exemple, un arrangement possible des calissons dans une boite hexagonale.
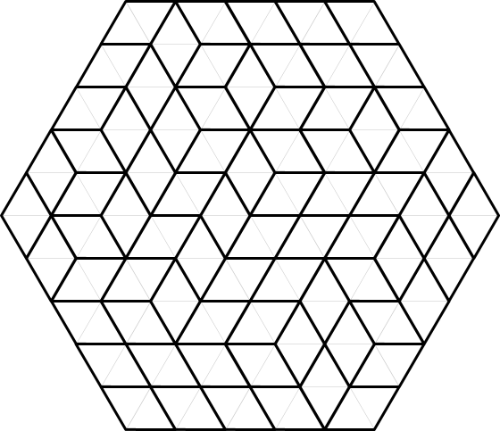
Si je colore les calissons selon leur orientation, on peut s'amuser à compter que, effectivement, il en a bien autant de chaque couleur.

Et là commencent la beauté du raisonnement : si je fais quelques rotations de cette figure, je peux distinguer que c'est équivalent à un tas de cubes, qu'on aurait posé dans un coin de pièce totalement carrelée avec des carrés.

Pour vous expliquer la manœuvre : initialement, la pièce est vide, on peut se convaincre qu'il y a autant de chaque couleur.
Selon votre vision de la 3D, vous pouvez avoir l'impression de voir un cube en creux ou un cube en plein.

Si j'ajoute un cube dans le coin de la salle, on ne change pas la proportion de faces dans les différentes orientations. Si je prend le raisonnement avec le sol : j'ai recouvert un carré du carrelage, mais la face supérieure du cube la compense.

Et si je continue de remplir ma salle en partant du fond, je recouvre à chaque fois 3 faces (et une de chaque couleur) avec mon nouveau cube, mais je fais apparaître 3 nouvelles faces (et c'est une de chaque couleur également)

Conclusion : peu importe votre arrangement de calissons dans la boite hexagonale, il y en aura autant dans chaque orientation.
calissons
D'après un tweet de brusicor :
https://twitter.com/brusicor02/status/1295410088837107712?s=20