Questões do Enem e OBMEP
INTRUÇÕES PARA RESPONDER AS QUESTÕES:
- Antes de resolver leia toda questão, ao final de cada pergunta tem uma instrução para resolver utilizando o GeoGebra.
- Quando finalizar a atividade é só clicar em Entregar ao final da atividade que será salvo o registro da atividade ao mesmo tempo que faz a entrega no Classroom automaticamente.
1. (OBMEP 2007, 1a Fase, Nível 3, Questão 18)
Qual dos gráficos abaixo descreve a variação da área do polígono BCDP em função da distância x=AP?
![[size=100]Fonte: OBMEP 2007, 1a Fase, Nível 3, Questão 18[/size]](https://www.geogebra.org/resource/hbjjkkxw/MWSVbsl62Kh5VIJ5/material-hbjjkkxw.png)
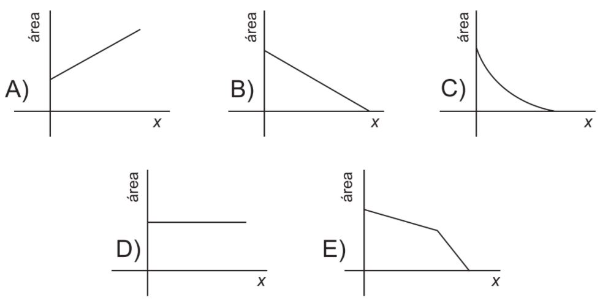
Assinale a alternativa correspondente ao gráfico que descreve a variação da área solicitada em função da distância x:
Instruções:
- Desloque o ponto P no quadrilátero, janela de visualização 1. E observe o movimento que descreve o ponto Q na janela de visualização 2, a medida que a distância m = AP se aproxima do ponto C reduzindo a área do polígono BCDP.
- Clique para marcar a opção "Lugar Geométrico" para visualizar o caminho que o ponto Q descreve em relação ao deslocamento do ponto P.
2. (OBMEP 2007, 1a Fase, Nível 3, Questão 4) A área do hexágono regular ABCDEF é 45 cm².
![[size=100]Fonte: OBMEP 2007, 1a Fase, Nível 3, Questão 4[/size]](https://www.geogebra.org/resource/jczgutqj/ngCEJRlQAFxd7RIh/material-jczgutqj.png)
Qual a área do triângulo sombreado?
Construa inicialmente o hexágono regular ABCDEF:
- Ative a ferramenta "Polígono Regular", na janela 5, e;
- Na sequência clique sobre os pontos A e B, nesta ordem, para construir o polígono com a dimensão do lado AB;
- Abrirá uma janela solicitando o número de vértices, no hexágono são 6 vértices.
- Selecione a ferramenta "Polígono", na janela 5, e;
- Clique sobre os três pontos que formam o triângulo, lembre-se que o polígono inicia e termina no mesmo ponto;
- Repita o procedimento para construir o segundo triângulo.
- Clique na janela 2 e ative a ferramenta "Interseção de Dois Objetos";
- Na sequência clique sobre o segmento AC e sobre o segmento BF para marcar o ponto G;
- Repita o procedimento clicando sobre os segmentos AE e BF para marcar o ponto H;
- Construa o triângulo AGH com a ferramenta "Polígono" e:
- Clique sobre este triângulo e na barra de estilo no canto superior direito (símbolo com três traços com um círculo e triângulo);
- Na opção de cor e transparência altere a cor azul com transparência 90;
- Ative a ferramenta "Área" na janela 8;
- Determine a medida da área deste triângulo azul clicando sobre ele com a ferramenta "Área" ativada.
3. (OBMEP 2018, 1a Fase, Nível 3, Questão 8)
A figura mostra o gráfico da função definida por . O ponto A tem coordenadas .
![[size=100]Fonte: OBMEP 2018, 1a Fase, Nível 3, Questão 8[/size]](https://www.geogebra.org/resource/byuh325t/JBpzoGJ8fNPmtQ0a/material-byuh325t.png)
Qual o valor de p?
Instruções:
- Inicialmente esboce o gráfico da função , digitando esta função no campo de entrada da janela de álgebra;
- Em seguida marque os pontos com abscissas em e , para isso, precisa determinar a imagem da função em cada um desses valores, uma forma de fazer isso, usando o recurso do GeoGebra é marcando um ponto C = (-2, f(-2)), onde f(-2) é a imagem da função quando tomamos x = -2, chame o outro ponto de D;
- Construa o segmento CD com a ferramenta "Segmento" (janela 3);
- Finalize determinando o Ponto A pertencente a este segmento e o eixo y.
4. (Enem 2017) Em um mês, uma loja de eletrônicos começa a obter lucro já na primeira semana. O gráfico representa o lucro (L) dessa loja desde o início do mês até o dia 20. Mas esse comportamento se estende até o último dia, o dia 30.
![[size=100][justify]Fonte: ENEM 2017[/justify][/size]](https://www.geogebra.org/resource/ukxcxvce/s0DUHULC0U44FQLb/material-ukxcxvce.png)
Fonte: ENEM 2017
A representação algébrica do lucro (L) em função do tempo (t) é:
Instruções:
Reproduzindo o gráfico no GeoGebra:
- Inicialmente utilize o campo de entrada para marcar os pontos que estão definidos no gráfico da função, nomeei-os de A e B;
- No campo de entrada digite o comando "Segmento( <Ponto>, <Ponto> )" e substitua "<Ponto>" pelos pontos nomeados;
- Em uma função afim, , sabemos que o valor de b, coeficiente linear, é o valor da ordenada da função quando intercepta o eixo y, isto é, ➔;
- O coeficiente angular, a, é determinado pelo quociente da variação do eixo y pela variação do eixo x, isto é, , ou ainda:
- Com base na interpretação do coeficiente a, utilize o GeoGebra pra determinar a medida desse coeficiente;
- De posse do valor de a e b da função f(x), digite a fórmula e verifique se o segmento pertence a esta função.