Problemas de ecuaciones
En esta página resolvemos problemas con la ayuda de ecuaciones de primer grado. La finalidad de este tema es aprender a transcribir un problema en una ecuación. Asumimos que ya sabemos resolver ecuaciones de primer grado.
Problema 1: Encontrar el número que cumple que la suma de su doble y de su triple es igual a 100.
Si x es el número que buscamos, su doble es 2⋅x y su triple es 3⋅x. La suma de los dos últimos debe ser 100:
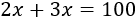Resolvemos la ecuación:
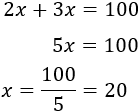El número buscado es 20.
En efecto, el doble de 20 es 40, su triple es 60 y ambos números suman 100.
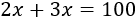Resolvemos la ecuación:
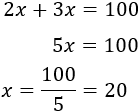El número buscado es 20.
En efecto, el doble de 20 es 40, su triple es 60 y ambos números suman 100.Problema 2: Si Ana es 12 años menor que Eva y dentro de 7 años la edad de Eva es el doble que la edad de Ana, ¿qué edad tiene Eva?
Si Ana es 12 años menor que Eva y dentro de 7 años la edad de Eva es el doble que la edad de Ana, ¿qué edad tiene Eva?Supongamos que x es la edad de Ana. Como Eva tiene 12 años más que Ana, su edad es x+12.
Dentro de 7 años, Ana tendrá la edad actual más 7, es decir, tendrá x+7. Del mismo modo, Eva tendrá (x+12)+7 = x+19.
Además, el doble de la edad de Ana será 2⋅(x+7).
Debemos resolver la ecuación
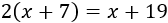Resolvemos la ecuación:
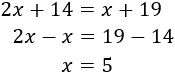Por tanto, la edad actual de Ana es 5 y la de Eva es 17. Dentro de 7 años, Ana tendrá 12 y Eva tendrá 24 (el doble que Ana).
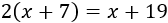Resolvemos la ecuación:
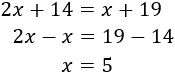Por tanto, la edad actual de Ana es 5 y la de Eva es 17. Dentro de 7 años, Ana tendrá 12 y Eva tendrá 24 (el doble que Ana).Problema 3: Si 25,5 es el 15% de una cierta cantidad, ¿cuál es el 80% de dicha cantidad?
Si x es la cantidad, su 15% se calcula multiplicando x por 15 y dividiendo entre 100. Como el 15% de x es 25,5, tenemos la ecuación
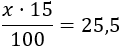La resolvemos:
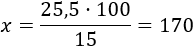Ahora calculamos el 80% de 170 multiplicando por 80 y dividiendo entre 100:
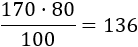Por tanto, el 80% es 136.
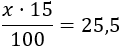La resolvemos:
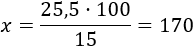Ahora calculamos el 80% de 170 multiplicando por 80 y dividiendo entre 100:
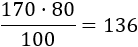Por tanto, el 80% es 136.Más problemas resueltos:
- Problemas de ecuaciones
- Problemas de sistemas de ecuaciones
- Ecuaciones de primer grado paso a paso
- Teorema de Pitágoras: problemas
- Potencias: propiedades y ejemplos
- Fracciones equivalentes y fracción irreductible
- Sistemas de ecuaciones (métodos)
- Ecuaciones de segundo grado paso a paso
- Problemas de mcm y MCD
- Problemas de MRU
- Integración por partes
- Introducción a las progresiones: aritméticas y geométricas
- Ecuaciones exponenciales explicadas
- Problemas y Ecuaciones .com