Eigenschaften von Exponentialfunktionen untersuchen
Die nachstehenden GeoGebra-Applets thematisieren Exponentialfunktionen der Form mit unterschiedlichen Basen .
Erledige die folgenden Aufgaben nacheinander.
Notiere dir deine gewonnenen Erkentnisse vorerst auf einem Schmierblatt.
Aufgabe 1: Schau dir das Bild an und überlege, welcher Zusammenhang zwischen einigen der monoton steigenden und fallenden Funktionsgraphen bestehen könnte.
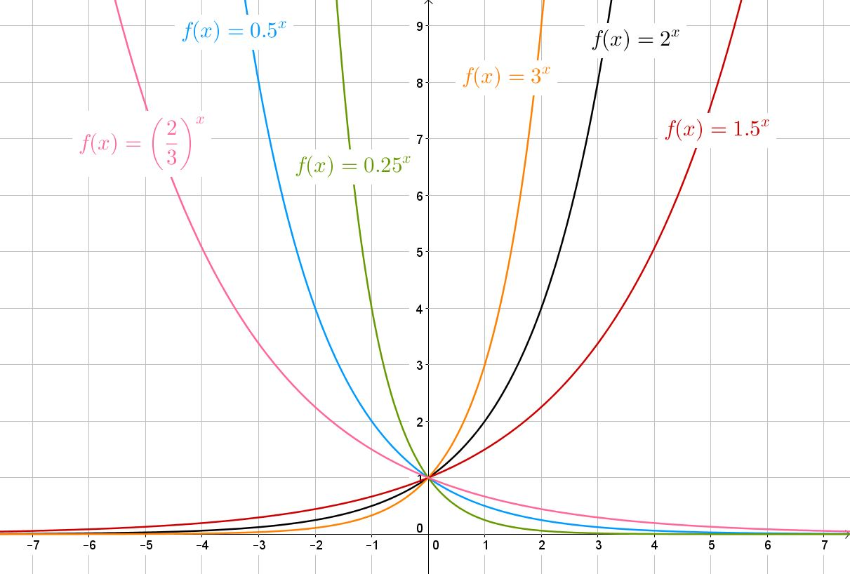
Aufgabe 2: Bewege den Schieberegler b2 so, dass der schwarze Funktionsgraph durch Spiegelung an der y-Achse aus dem orangenen hervorgeht.
Aufgabe 3: Bewege den Schieberegler b2 so, dass der schwarze Funktionsgraph durch Spiegelung an der y-Achse aus dem orangenen hervorgeht.
Aufgabe 4: Bewege den Schieberegler b2 so, dass der schwarze Funktionsgraph durch Spiegelung an der y-Achse aus dem orangenen hervorgeht.
Aufgabe 5: Verschiebe die Schieberegler b1 und b2 so, dass die Funktionen durch Spiegelung an der y-Achse auseinander hervorgehen. Versuche mindestens drei Paare an Funktionsgleichungen zu finden.
Aufgabe 6: Zusammenfassung
Du hast bestimmt herausgefunden, dass Exponentialfunktionen mit unterschiedlichen Basen gewissen Zusammenhänge haben. Nun geht es daran, deine erarbeiteten Erkentnisse festzuhalten.
Wir betrachten dabei die Exponentialfunktionen zur Basis 2 und zur Basis 0,5.
Lege deine Mitschriften zu folgenden Punkten (in Tabellenform) an:
- Definitions- und Wertebereich
- Nullstellen und Schnittpunkt mit der y-Achse
- Monotonieverhalten
- Asymptoten
Zeichne abschließend zu beiden Exponentialfunktionen und die Funktionsgraphen. Lege das Koordinatensystem wie folgt an: 1 Einheit = 1 cm / x-Achse von -3 bis 3 / y-Achse von 0 bis 8