Transformações no plano
Definição: Uma transformação afim M(x,y) = A(x,y) + é uma composição de uma transformação linear L(x,y) = A.(x,y) e uma translação T(x,y) = (x,y) + . Onde a matriz A é uma matriz 2x2 regular
A=
as equações da transformação afim M são com .
O jacobiano da transformação afim M é
JM= = =
As transformações lineares canônicas são:
---> Explicar o que é uma transformação linear geral<----------
Apresentamos abaixo uma lista de applets com cada tipo de transformação, aberta para o aluno manipular e observar cada tipo de transformação..
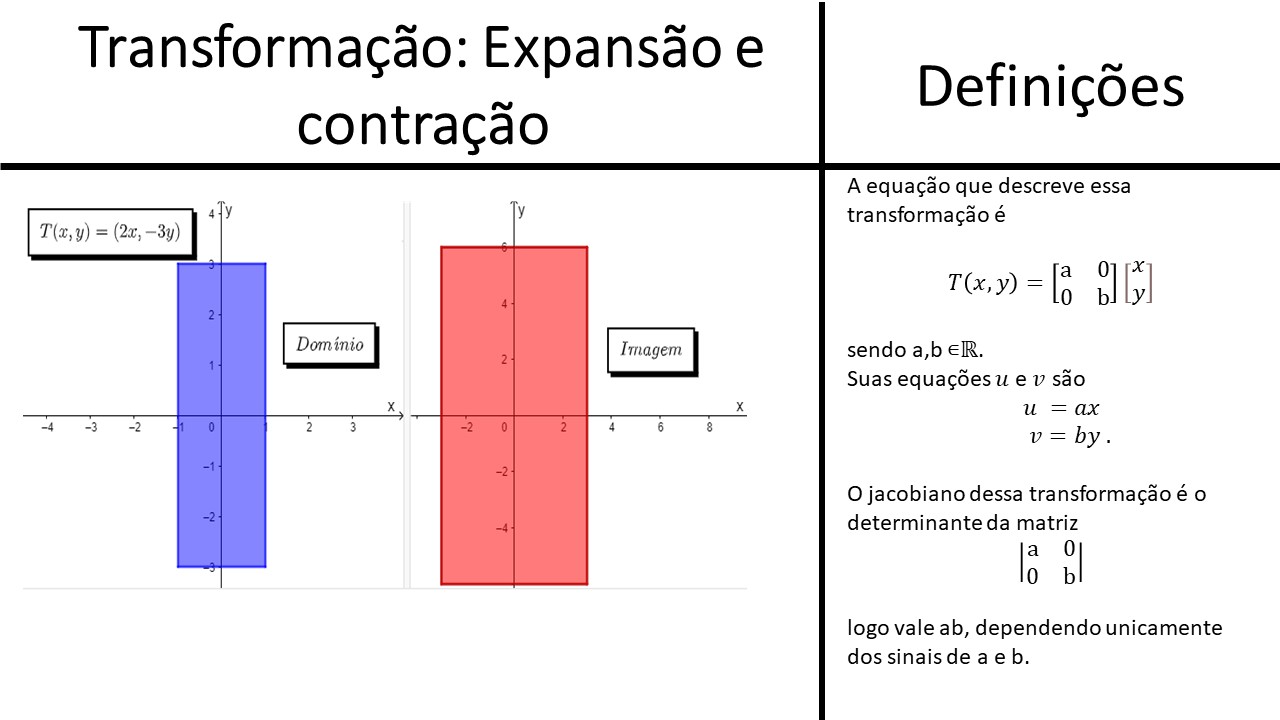
Expansão e contração : Autovalores reais distintos
Equações da transformação:
Temos que e
Seu jacobiano vale .
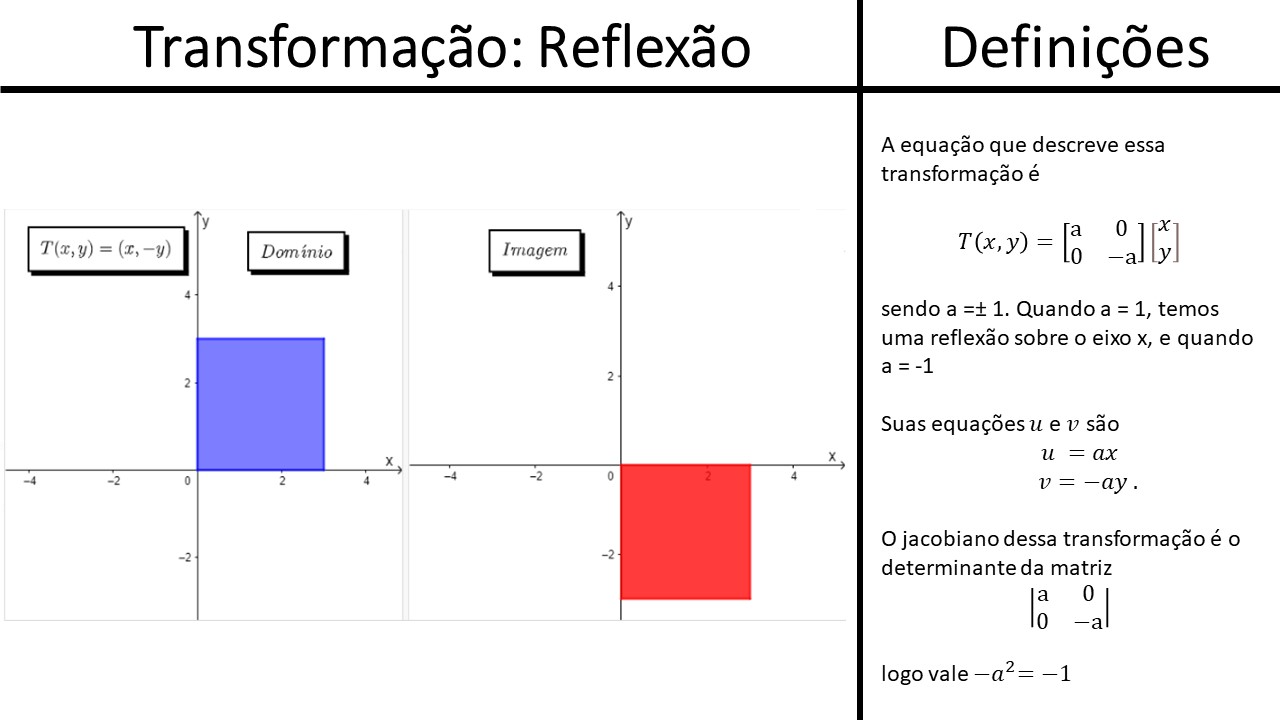
Reflexão: Autovalores 1 e -1
Equações da transformação:
Temos que e
Seu jacobiano vale
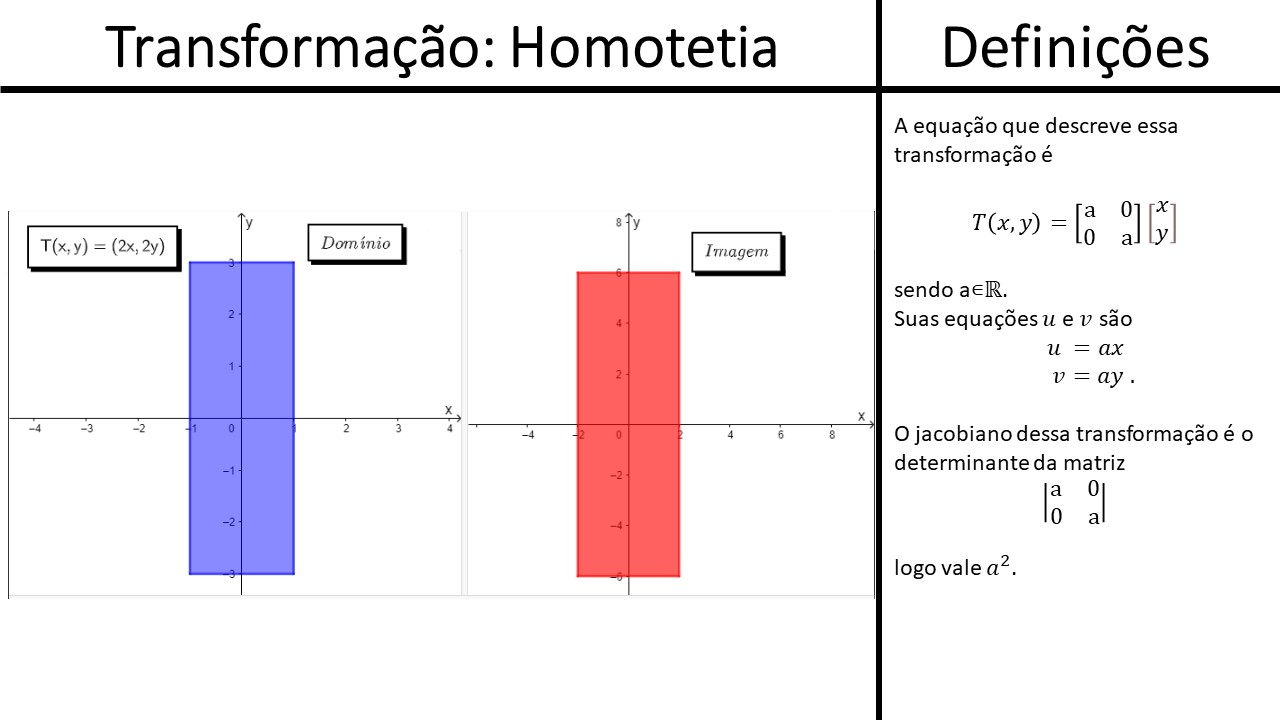
Homotetia: Autovalor duplo com dois vetores linearmente independentes
Equações da transformação:
Temos que e
Seu jacobiano vale
Autovalor duplo com um "único autovetor"
Equações da transformação:
Temos que e
Seu jacobiano vale
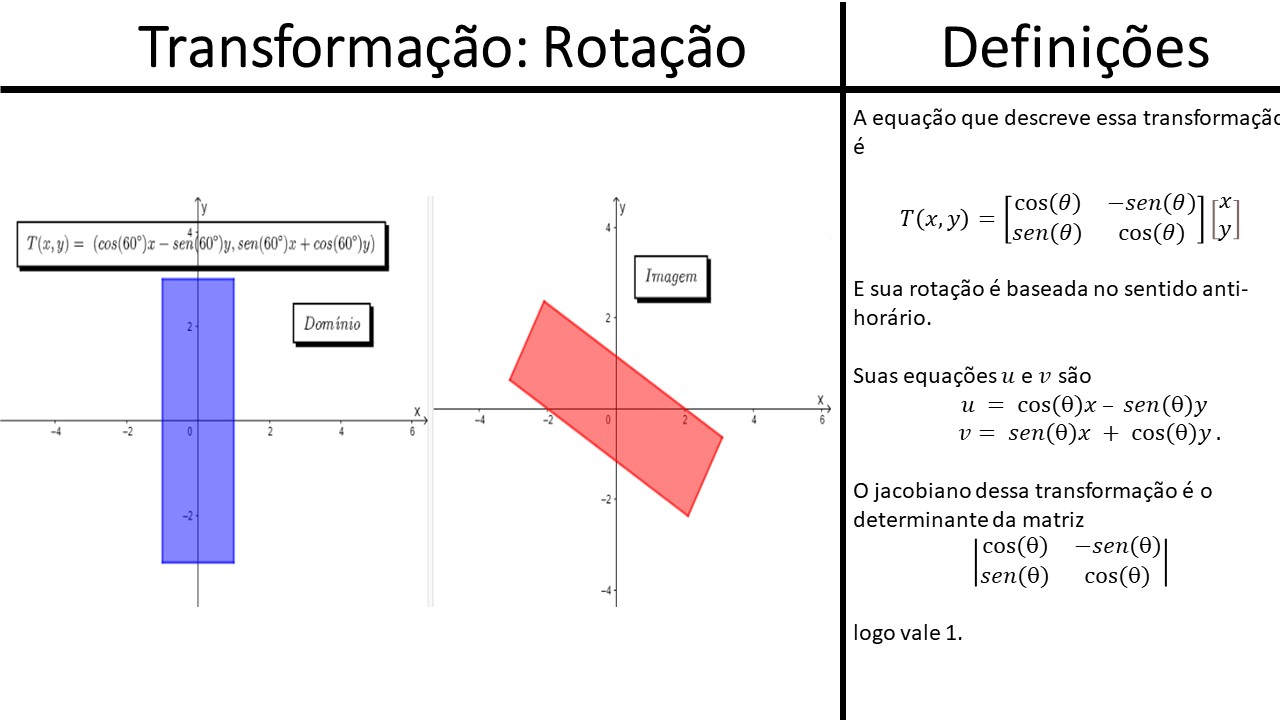
Autovalores complexos
Equações da transformação:
Temos que e
Seu jacobiano vale
Equações da transformação:
Temos que e