13.多角形の面積
1.多角形の面積
このページは電子ブック「探求 数学Ⅰ」の一部です。
<三角形の面積と正弦定義>
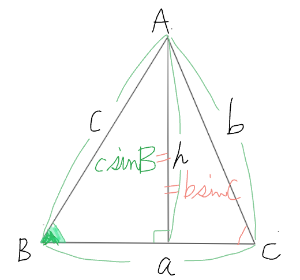
・頂点Aから辺aにおろした高さをhとする。
正弦定義からだから、h=c・sinB=b・sinCとかける。
三角形ABCの面積はa×h÷2=
同様にして、辺bに垂線をおろして、
三角形ABCの面積はb×高さ÷2=
サイクリックに整理すると、
三角形の面積=2辺の積×間の角の正弦。
(例)2辺が3,4で間の角が150°の三角形の面積は?
sin150°=sin30°=1/2だから、1/2・3・4・1/2=3。
<平行四辺形の面積>
平行四辺形の面積=2辺の積×間の角の正弦。
(例)対角線が10,12で60°で交わる平行四辺形の面積は?
対角線で区切られる4つの三角形のうちの1つは60°を10÷2=5,12÷2=6が挟む。
sin60°=.
<多角形の面積>
多角形は三角形に分割して面積を求める、という方針を立てることもできる。
<(参考)余弦定理からヘロンの公式を作ろう>
三角形の面積は上記のようにS=1/2bc・sinAで求められる。
一方で、cosA=xとすると、sinA=√(1-x2)=√(1+x)(1-x)と表すことができるね。
ここでx=cosA=(b2+c2-a2)/(2bc)を上の式に代入してみよう。
・sinA=
=
だから、S==
=
=

2.三角形の内心と角の二等分線
<内心>
三角形ABCの2つの頂点の角の2等分線の交点Iを、[内心(incenter)]という。
Iから3辺におろした垂線の足を、辺a,b,cの順に、D,E,Fとする。
ID=IE=IFになる。これをrとする。
中心I、半径rの円が三角形ABCの[内接円(incircle)]になる。
円外から接点までの長さは等しいので、AF=AE=x,BF=BD=y,CD=CE=zとおける。
<内接円の半径>
3辺a,b,cを底辺として、高さをrとする三角形の面積の合計は、三角形全体の面積Sと等しい。
だから、r(a+b+c)/2=S。だから、
<角の2等分線定理>
三角形ABCの頂点Aを2等分する線と対辺aとの交点をDとする。
点Dから残りの辺b,cへおろした垂線の長さhは等しい。
・2辺b,cを底辺として、高さをhとする三角形ABDと三角形ACDの面積比は、
bh/2:ch/2=b:c=DC:DBだから、角の2等分線は2等分した角をはさむ辺の比に残りの辺を分ける。
・三角形ABDと三角形ADCの面積の和は三角形全体の面積Sと等しい。
角A=2kとする。面積の2倍についての式ができる。
cd・sink+bd・sink=bc・sin2kだから、となる。

(例)
「c=2,b=3,角A=120°のときの角Aの二等分線ADの長さ」は?
、となる。その積は
(例)
「c=6,b=8,角A=60°のときの角Aの二等分線ADの長さ」は?
、となる。その積は
(例)
「c=2,b=3,a=4の三角形ABCの内心をIとするときAIの長さ」は?
角Aの2等分線をADとすると、角Aをはさむ辺の比でaを比例配分して、BD=4×2/(2+3)=8/5。
三角形ABCの3辺から余弦定理でcosB=(c2+a2-b2)/(2ca)=(4+16-9)/(2・2・4)=11/16。
三角形ABDで余弦定理でAD2=AB2+BD2-2AB・BD・cosB=4+(8/5)2-2・2・(8/5)・(11/16)=54/25。AD=3√6/5
角Bの2等分線がBIは、ADをAB:BD=2:8/5=5:4に比例配分して3√6/5×5/(5+4)=√6/3。
(別解 数学Ⅱ)
cosA=(b2+c2-a2)/(2bc)=(9+4-16)/(2・3・2)=-1/4。sinA=√(1-1/16)=√15/4
半角の公式からsinA/2=√((1-cosA)/2)=√(5/8)=√10/4 。
AD=sinA/sin(A/2) ・bc/(b+c)= (√15/4)/(√10/4)・3・2/(3+2)=3√6/5 角Bの2等分線がBIは、ADを
AB:BD=2:8/5=5:4に比例配分して3√6/5×5/(5+4)=√6/3。