Power Series
A power series is a type of series with terms involving a variable. More specifically, if the variable is x, then all the terms of the series involve powers of x. As a result, a power series can be thought of as an infinite polynomial. Power series are used to represent common functions and also to define new functions. Since the terms in a power series involve a variable x, the series may converge for certain values of x and diverge for other values of x.
For a power series centered at x=a the value of the series at  is given by
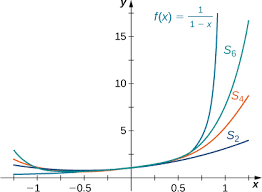
is given by  Therefore, a power series always converges at its center. Some power series converge only at that value of x. Most power series, however, converge for more than one value of x. In that case, the power series either converges for all real numbers x or converges for all x in a finite interval. For example, the geometric series
Therefore, a power series always converges at its center. Some power series converge only at that value of x. Most power series, however, converge for more than one value of x. In that case, the power series either converges for all real numbers x or converges for all x in a finite interval. For example, the geometric series  converges for all x in the interval
converges for all x in the interval  but diverges for all x outside that interval. We now summarize these three possibilities for a general power series.
but diverges for all x outside that interval. We now summarize these three possibilities for a general power series.
A power series is a series representation of a function as an infinite sum of terms involving powers of a variable (usually (x)). Each term in the series is a constant multiplied by a power of (x). The general form of a power series is:
cnxn form n=0 to ; where (cn) are constants and (x) is the variable.
Example: The Power Series for (ex)
One of the most famous examples of a power series is the Taylor series expansion for the exponential function (ex). The power series representation of (ex) is:
. . . when n= 0 to
In this power series, each term is obtained by taking (x) raised to a non-negative integer power (xn) and dividing it by the factorial of (n)(n!)). The constant coefficients cn are cn=
The power series expansion of (ex) converges for all values of (x) since the exponential function (ex) is well-behaved and has a finite value for any real (x). The series represents an infinite sum of terms that approach the exponential function (ex) as more terms are included.
The first few terms of the power series can approximate the exponential function for small values of (x). As more terms are added, the approximation becomes more accurate. The power series expansion is particularly useful for calculating values of (ex) to high precision and for extending the definition of (ex) to complex numbers.
Note that power series representations are not always convergent for all values of (x), and the convergence of a power series depends on the behavior of the function it represents. However, the power series expansion for (ex) is an example of a well-behaved and convergent power series.