Ableitung als Grenzwert (h-Methode)
Einordnung
Ziel ist es, den lokalen Anstieg einer Funktion an einer Stelle als Grenzwert zu berechnen und die h-Methode zu visualisieren.
Aufgaben
- Beschreiben Sie den Grundgedanken der schrittweisen Annäherung an die Tangente an den Graphen von f im Punkt P0.
- Warum muss h ungleich Null sein?
- Welcher Grenzprozess wird gesucht? Formulieren Sie "Wenn ..., dann ...." - Sätze.
- Berechnen Sie den Anstieg der Tangente im Punkt P0 durch Grenzwertberechnung.
- Kontrollieren Sie Ihre Ergebnisse und Ändern Sie die Stelle x0. Arbeiten Sie erneut.
Ergebnisse und Fachsprache
Der Anstieg der Sekante an der Graphen einer Funktion f an der Stelle x0 beim Wert h () wird auch als Differenzenquotient bezeichnet. Bei jeder Stelle x0 hängt der Wert des Differenzenquotienten von der Hilfsgröße h ab.
Wenn der Grenzprozess beim Differenzenquotienten zu einen Grenzwert führt, nennt man diesen Grenzwert auch Differenzialquotient von f an der Stelle x0.
Dieser Differenzialquotient wird als erste Ableitung von f an der Stelle x0 bezeichnet und formal mit f'(2) gekennzeichnet.
Die Funktion f heißt an dieser Stelle x0 differenzierbar.
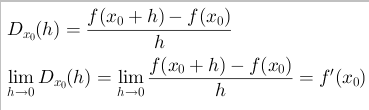
Für das oben bearbeitete Beispiel gilt also:
- Für die Funktion hat der Grenzwert des Differenzenquotienten an der Stelle 1 für h gegen Null den Grenzwert 2.
- Die Funktion mit hat an der Stelle 1 den Anstieg 2.
- Die Funktion mit hat an der Stelle 1 die erste Ableitung 2.
- Die erste Ableitung der Funktion an der Stelle 1 hat den Wert 2
- Für gilt: .