Exploring the scalar product of two vectors

Author:kokming lee

Topic:Vectors 2D (Two-Dimensional)

We will start by reviewing a few main concepts before we explore the aim of this investigation. Review Question 1.

What is the symbol for magnitude of vector a?

Select all that apply

Check my answer (3)

Review Question 2

Find the magnitude of the vector v = .

Check my answer

Introduction

In this exploration we will explore the geometric definition of a scalar product of two vectors in 2D. The results can be generalized to 3D as well. The scalar product is also known as the dot product. As a reminder, we know the algebraic definition of a scalar product of

and

is defined as

Question 1. Application of algebraic definition.

If the two vectors are and then find . Show your working,

Check my answer

Change the points and record your observations in the table. What do you observe between the angle and the scalar product?

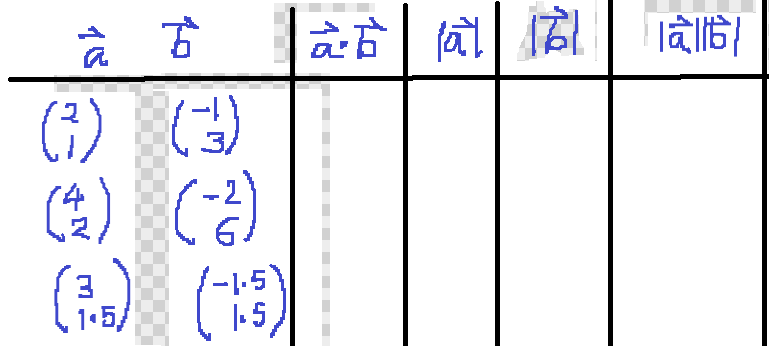
Use the Geogebra applet here to complete the table above.

Note.

For a vector

you can enter this as <2, 1> in the Geogebra table. Please note that <2, 1> is not a conventional notation. We are using it here due the input limitation into Geogebra table.

Questions for Investigation 1.

1. What do you notice? 2. Which terms are proportional? 3. How can you explain this proportionality?

Check my answer

Now expand the table in your Geogebra applet with this investigation. You can use <4,0> to denote a vector 4i + 0j.

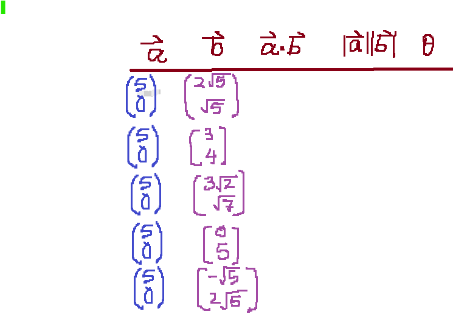
Questions for Investigation 2. Please use GDC or appropriate technology to answer these questions.

1.Use data from Investigation 2 only. Plot a graph with angle in the horizontal axis and the associated scalar product in the vertical axis. 2. Describe the pattern or trend on this curve. 3. Use an appropriate regression to find the equation of this curve.

Check my answer