Extremos de funciones de dos variables
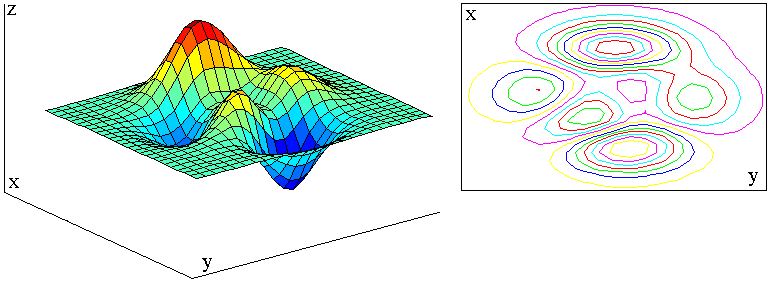
Teorema del valor extremo
Sí f es una función contínua de dos variables x y y, definida en una región acotada R en el dominio, entonces:
- Existe por lo menos un punto en R, en el que f toma un valor mínimo.
- Existe por lo menos un punto en R, en el que f toma un valor máximo.
Extremo en una región R
Extremos relativos
Un punto (x0, y0) de una función es crítico cuando satisface las siguientes condiciones:
- fx(x0, y0) = 0 y fy(x0, y0) = 0
- fx(x0, y0) o fy(x0, y0) no existe.
¿Cuál tipo de extremo?
Existen tres tipos de extremos relativos: máximo, mínimo y punto de silla.
Nota: Para cualquier otro caso, se debe analizar en una región específica.
Criterio de la segunda derivada
