4.3. As funções e suas aplicações
Por que aprender funções? Na ciência e nas mais variadas atividades humanas, as funções são usadas para descrever e estudar a relação entre grandezas.
Assista ao vídeo.
Exemplo 1: O gasto com combustível é função do número de litros colocados no tanque do automóvel.

Exemplo 2: A dose de remédio dada a uma criança, muitas vezes, é função da massa da criança.

Exemplo 3: O juro pago por um empréstimo é calculado em função da quantia emprestada.

As funções têm aplicações nas situações do cotidiano e do trabalho. Acompanhe as situações apresentadas:
Primeira situação:

No açougue, o quilograma de determinado tipo de carne custa R$ 6,00. O preço a pagar y é função da quantidade de carne comprada x. veja a tabela:
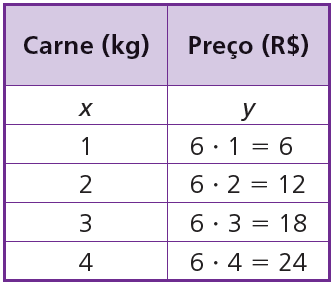
A cada valor de x corresponde um único valor de y.
A lei de formação dessa função é y = 6x.
Lembre que: x e y são as variáveis da função.
A lei de formação da função estabelece a relação matemática entre x e y. Vamos aplicá-la para responder a algumas questões.

Observe que, nesse exemplo de função, x não pode assumir valores negativos, pois uma medida de massa nunca é negativa.
No açougue o funcionário digita na balança o preço do kg de carne (R$ 6,00) e coloca a carne sobre o prato da balança que registra a massa (é o valor de x).

A balança calcula automaticamente 6 . x e apresenta no visor o valor a pagar, que é o valor de y.

Responda:
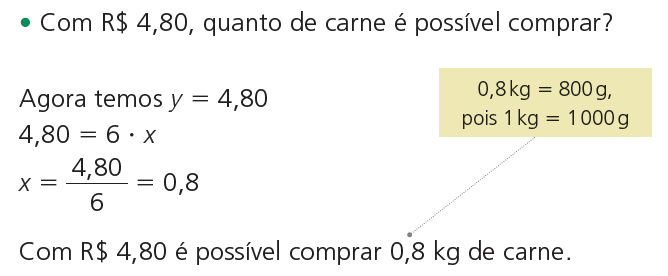
Quanto se paga por 2,5 kg dessa carne?
Segunda situação.


Em um parque de diversões, os visitantes pagam R$ 15,00 pelo ingresso e R$ 3,00 para brincar em cada uma das 20 atrações disponíveis. A quantia p gasta pelo visitante depende do número de atrações n que ele escolher e pagar.
Lembre que: n e p são as variáveis dessa função
Podemos representar a relação entre n e p pela fórmula p = 15 + 3n.
A cada valor de n nesse intervalo corresponde um único valor a pagar p. Então p é função de n.
Responda:

A cada valor de n nesse intervalo corresponde um único valor a pagar p. Então p é função de n.
Situação 3:
A cada valor de n nesse intervalo corresponde um único valor a pagar p. Então p é função de n.
Uma fábrica produz placas de aço na forma de retângulos. As medidas variam; no entanto, a medida do comprimento tem sempre 5 cm a mais do que a medida da largura. Quantos centímetros quadrados de aço são gastos em cada placa?
2) Nessa função, qual é o menor valor que podemos ter para p? Explique esse valore.

Qual deve ser a medida x para que a área da peça retangular seja de 104 cm²?
Basta fazer y = 104 cm² na lei de formação da função:
y = x² + 5x
104 = x² + 5x
Obtivemos uma equação do 2º grau. Vamos resolvê-la para encontrar x.
Reescrevendo a equação:
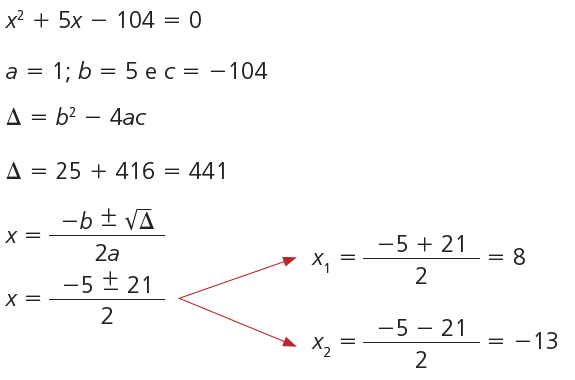
Reescrevendo a equação:
Se os lados do retângulo medem (x + 5) e x, sua área é y = (x + 5) * x.
Aplicando a propriedade distributiva obtemos y = x² + 5x.
A cada valor de x corresponde um único valor de y. então y é função de x.
Podemos montar uma tabela com alguns valores dessa função.
Consideramos somente a solução positiva, pois x é a medida do lado do retângulo.
Então, para que a área da peça seja de 104 cm², devemos ter x = 8 cm.
