Restklassen IP/ℤ₇ - lineares Gleichungssystem
A erweiterte Matrix {A b}, (aus Ax = b)
ℤp Restklasse p=7
IPi definiere Einheitmatrizen für Zeilenadditionen und Zeilenaustausch
Müssen händisch an die Eingabematrix angepasst werden - werden von links multipliziert
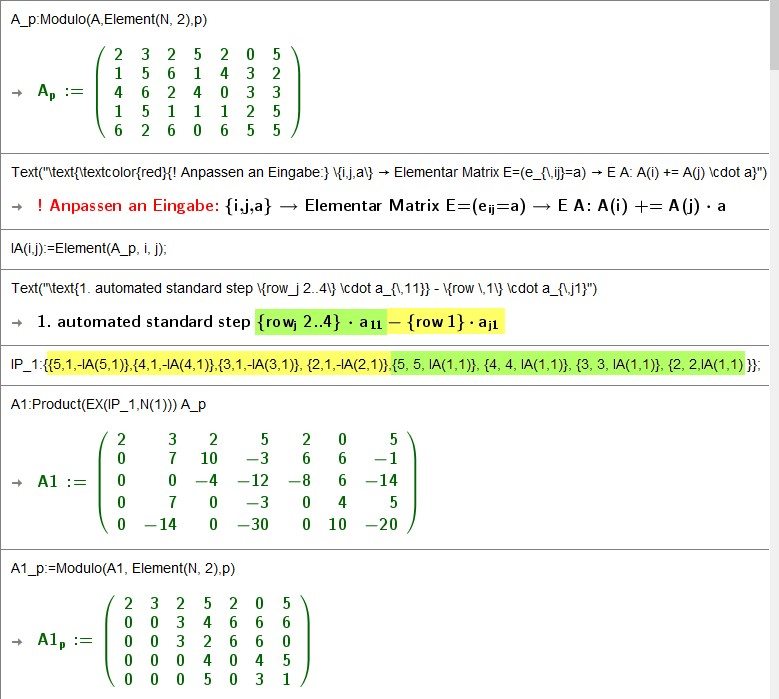
{ i , j , a } Zeilenadditionen: {Zeile i} += {Zeile j} a
{ j , j , a } Zeilenmultiplikationen: {Zeile j} = {Zeile j} a
{ i , j } Zeilentausch i j { i < j }
Aip Ai mod p - ist die Restklassen Anwendung
Wenn sie eine neue Aufgabe bearbeiten, dann überschreiben sie die Matrix Zeile (5) durch Ändern oder Copy&Paste. Setzen sie die Bearbeitungsschritte (Schablonen der Elementarmatrizen)
IPi auf {{1,1,1},.....,{1,1,1}}
das geht schneller als bei neuen Eingaben die Klammern {} korrekt zu setzen.
Oder kopieren sie eine id-Schablone ein
IP_1...4 :{{1, 1, 1}, {1, 1, 1}, {1, 1, 1}, {1, 1, 1}, {1, 1}};
wo sie dann nur noch die benötigten Elementarmatrizen mit aktuellen Werten überscheiben!
Unter 5.x werden die Schritte von rechts (zuerst) nach links und in 6.x von unten (zuerst) nach oben abgearbeitet.
Modulo Inverse (p prime)
Um einen (Diagonal-) Eintrag a auf 1 zu setzen suche ich einen Faktor k der bei der Multiplikation auf eine Restklasse 1 führt, also eine Zahl k a mod p =1 erzeugt, die Faktoren können sie anzeigen mit
Sequence( Element(KeepIf(floor(x)==x, (Sequence(p) p +1)/(a)),1), j,1,p-1)
p=7=> {8, 4, 5, 2, 3, 6}
z.B. eine 3 * 5 = 15 mod 7 = 1 ggf. die Zeile k damit multiplizieren {k,k,5}
oder die Funktion FaktorMod1(a) benutzen - siehe Beispiel Anwendung.
Falls die simple Suche FaktorMod nicht ausreicht wäre ein erweiterter Euklid angesagt!
Wenn sie mit den 4 Schritten nicht auskommen müssen sie vor A4 einen neuen Schritt einfügen, A4 und folgende sollten nicht geändern werden und der letzte Schritt bleiben, weil diese Namen in der Auswertung verwendet werden.
Funktionen E(),T(), IE() stellen nach v.745 ihre Funktion ein (bug_report erfolgt ), ersetzt durch EX()!
Beispiel Anwendung

Example running 5.x: first column step